с объяснением пжпжпжпжпжпж

Ответы
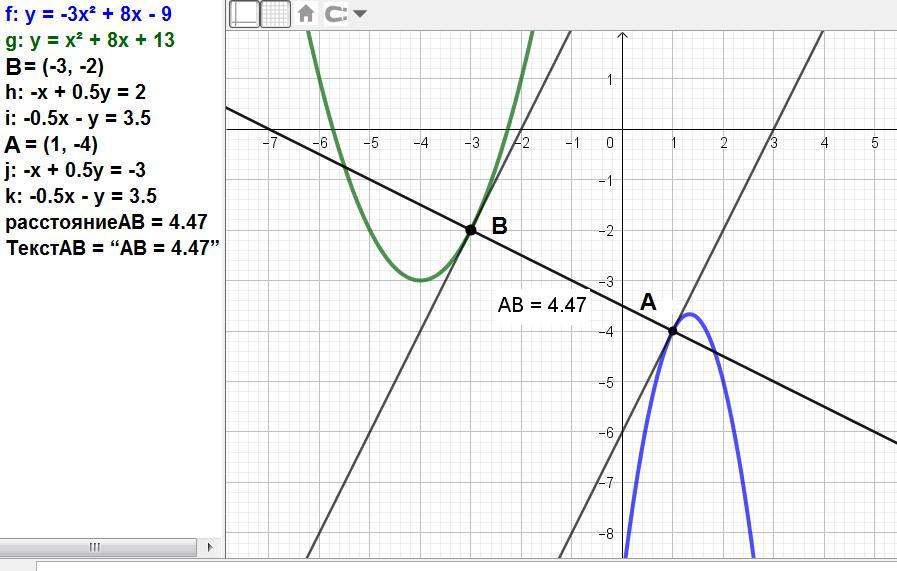
Решение:
Отметим по точке на параболе.
На той, что смотрит ветвями вниз, пусть это точка А:
Координаты по оси Ох обозначим a, значение функции выведем через а.
A(a; -3a^2+8a-9).
На другой точке В координаты по оси Ох обозначим b, значение функции выведем через b: B(b; b^2+8b+13).
Предположим точки А и В самые близкие точки двух кривых. Из геометрических соображений, связанных с выпуклостью, ясно, что наименьшее расстояние между указанными точками достигается в том и только в том случае, если касательные к параболам в этих точках параллельны.
Находим производные функций (они определяют угол наклона касательной к кривой к оси Ох): y’(A) = -6a+8, y’(B) = 2b+ 8.
Отсюда -6a+8=2b+ 8; b=-3a;
Теперь b обозначим через a.
B(-3a; 9a^2-24a+13).
Расстояние между точками А и В.
Определим разность координат:
Δx = (-3a) - a, Δy = (9a^2-24a+13) – (-3a^2+8a-9) = (-4a; 12a^2-32a+22).
Определяем расстояние АВ:
r = √(-4a)^2+(12a^2-32a+22)^2 ) =
= √(16a^2+(12a^2-32a)^2-44(12a^2-32a)+484) =
= √(16a^2+144a^4-768a^3+1024a^2+528a^2 + 1408a+484 )=
= √(144a^4-768a^3+1568a^2-1408a+484).
Находим минимум полученной функции, приравнивая нулю производную подкоренного выражения (при нуле под корнем и функция будет равна нулю).
(144a^4-768a^3+1568a^2-1408a+484)' = 576a^3-2304a^2+3136a-1408 =
= 64(9a^3-36a^2+49a-22) = 0.
На 64 можно сократить, тогда производная примет вид:
9a^3-36a^2+49a-22 = 0.
Так как сумма коэффициентов уравнения равна нулю, значит оно имеет корень a=+1.
Разложим кубическое уравнение на множители, разделив его на (a – 1).
Получим 9a^3-36a^2+49a-22 = (a – 1)(9a^2-27a+22).
Ищем дискриминант квадратного трёхчлена:
D = (-27)^2-4*9*22=729-4*9*22 = 729-36*22 = 729-792 = -63.
Дискриминант меньше 0, уравнение не имеет корней, значит, корень a = 1 единственный.
Определяем свойство полученной критической точки уравнения по знакам производной левее и правее точки a = 1.
a = 0 1 2
f’ = -22 0 4.
Как видим, в точке а = 1 имеем минимум функции.
Тогда расстояние между точками А и В равно
r(1) = √(144-768+1568-1408+484) = √20.
Ответ: √20 = 2√5.