Question

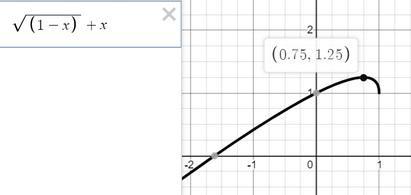
Найдите точки экстремумов функции у =х+под корнем 1-х
ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО НУЖНО!!!!​

Answer 1

Ответ:

Объяснение:

ОДЗ 1-x ≥ 0 ⇒ x ≤ 1

точки экстремумов ищем при помощи первой производной

$\displaystyle y'(x) = (x+\sqrt{1-x} )' = 1+\frac{1}{2\sqrt{1-x} } *(-1) = \frac{2\sqrt{1-x}-1 }{2\sqrt{1-x} }$

y'(x) = 0   ⇒   $\displaystyle 2\sqrt{1-x} -1 =0 \quad \sqrt{1-x} =0.5\quad 1-x =0.25\qquad x_0= 0.75$

это критическая точка.

чтобы понять какая это точка - минимум или максимум - по правилам надо использовать достаточное условие экстремума функции и посмотреть на знак второй производной в критической точке

$\displaystyle y''(x) = \bigg (1-\frac{1}{2} (1-x)^{-1/2}\bigg )'=0-\frac{1}{2} *(-\frac{1}{2} )(1-x)^{-1/2-1}*(-1)=-\frac{1}{4(1-x)^{3/2}} \\\\y''(0.75) = -2 \quad < 0$

если вторая производная в критической точке < 0, то у нас x₀ = 0.75 точка максимума функции

ответ

точка экстремума функции - точка x₀ = 0.75 и это точка максимума

и у(0,75) = 1,25