Решите уравнение_____________
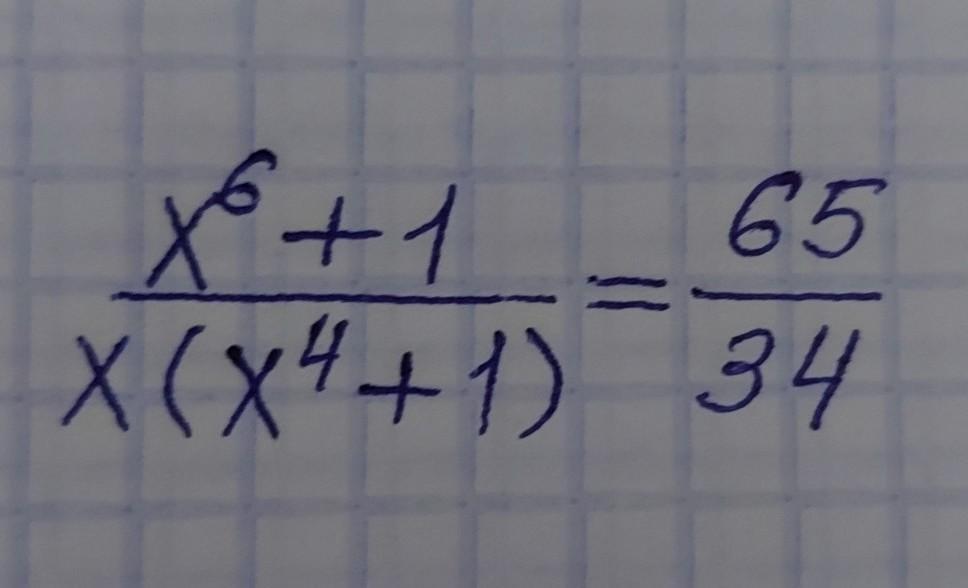
Ответы
Ответ:
x1 = 2; x2 = 1/2
Объяснение:
По правилу пропорции:
34(x^6 + 1) = 65x(x^4 + 1)
34x^6 - 65x^5 - 65x + 34 = 0
34x^6-68x^5 + 3x^5-6x^4 + 6x^4-12x^3 + 12x^3-24x^2 + 24x^2-48x - 17x+34 = 0
34x^5(x-2) + 3x^4(x-2) + 6x^3(x-2) + 12x^2(x-2) + 24x(x-2) - 17(x-2) = 0
(x-2)(34x^5 + 3x^4 + 6x^3 + 12x^2 + 24x - 17) = 0
x1 = 2
34x^5 - 17x^4 + 20x^4 - 10x^3 + 16x^3 - 8x^2 + 20x^2 - 10x + 34x - 17 = 0
17x^4(2x-1) + 10x^3(2x-1) + 8x^2(2x-1) + 10x(2x-1) + 17(2x-1) = 0
(2x-1)(17x^4 + 10x^3 + 8x^2 + 10x + 17) = 0
x2 = 1/2
17x^4 + 10x^3 + 8x^2 + 10x + 17 = 0
Это симметричное уравнение, решается делением на x^2
17x^2 + 10x + 8 + 10/x + 17/x^2 = 0
17(x^2 + 1/x^2) + 10(x + 1/x) + 8 = 0
Делаем замену y = x + 1/x.
Заметим, что |y| ≥ 2 при любом х.
То есть y € (-oo; -2] U [2; +oo)
Дальше.
y^2 = (x + 1/x)^2 = x^2 + 2x*1/x + 1/x^2 = x^2 + 1/x^2 + 2
Подставляем.
17(y^2 - 2) + 10y + 8 = 0
17y^2 + 10y - 26 = 0
D = 100 - 4*17(-26) = 100 + 1768 = 1868 = (2√467)^2
y1 = (-10 - 2√467)/34 = (-5 - √467)/17 ≈ -1,565 не € ОДЗ.
y2 = (-10 + 2√467)/34 = (-5 + √467)/17 ≈ 0,976 не € ОДЗ.
Таким образом, оба корня не подходят.
Ответ:
1/2; 2
Объяснение:
,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
