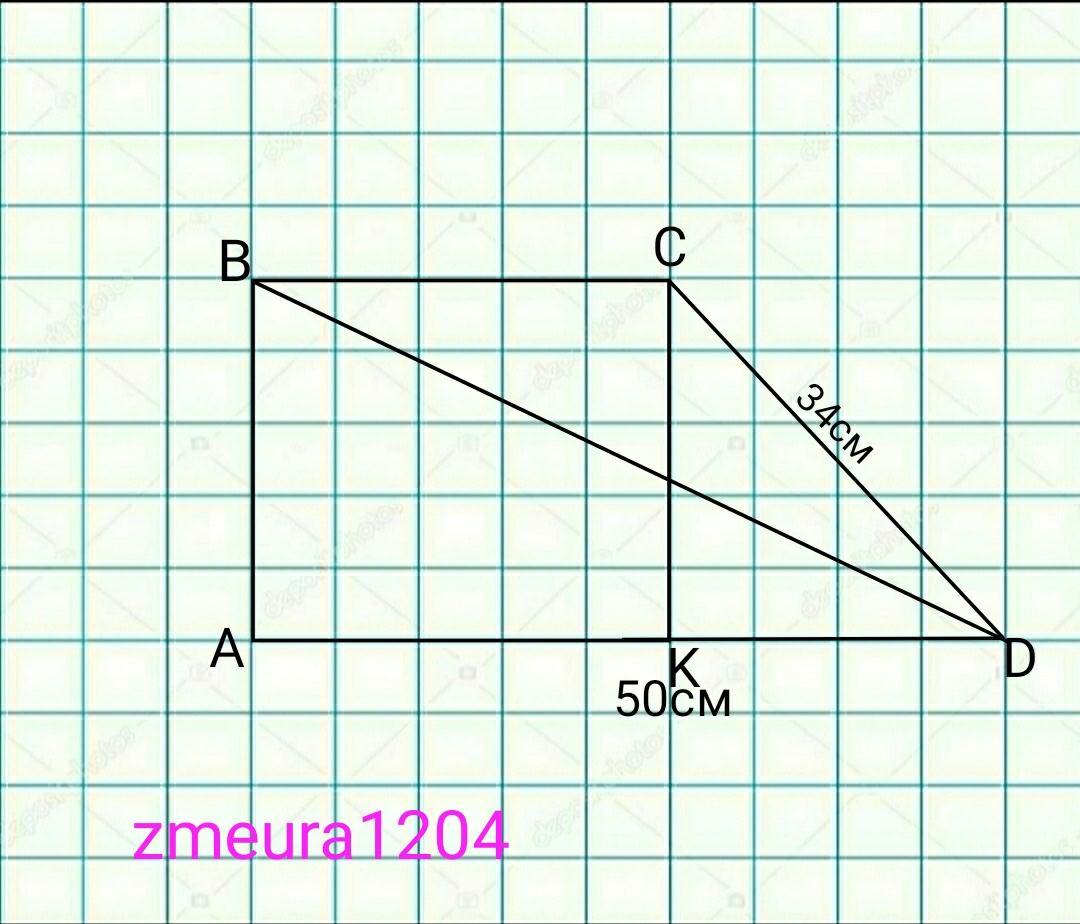
Большее основание прямоугольной трапеции равно 50 см, а большая боковая сторона равна 34 см. Найдите периметр трапеции, если большая диагональ является биссектрисой острого угла.
Ответы
Ответ:
148см
Объяснение:
<ВDC=<BDA, т.к. BD- биссектрисса.
<ВDA=<CBD, внутренние накрест лежащие при параллельных прямых
ВС||АD секущей ВD.
<ВDC=<CBD,
∆ВCD- равнобедренный треугольник, углы при основании равны.
ВС=СD=34см.
АК=ВС=34см
КD=AD-AK=50-34=16см
∆СКD- прямоугольный треугольник
По теореме Пифагора
СК=√(СD²-KD²)=√(34²-16²)=√(1156-256)=
=√900=30см
АВ=СК=30см
Р=АВ+ВС+CD+AD=30+34+34+50=148см
Ответ:
148 см
Объяснение:
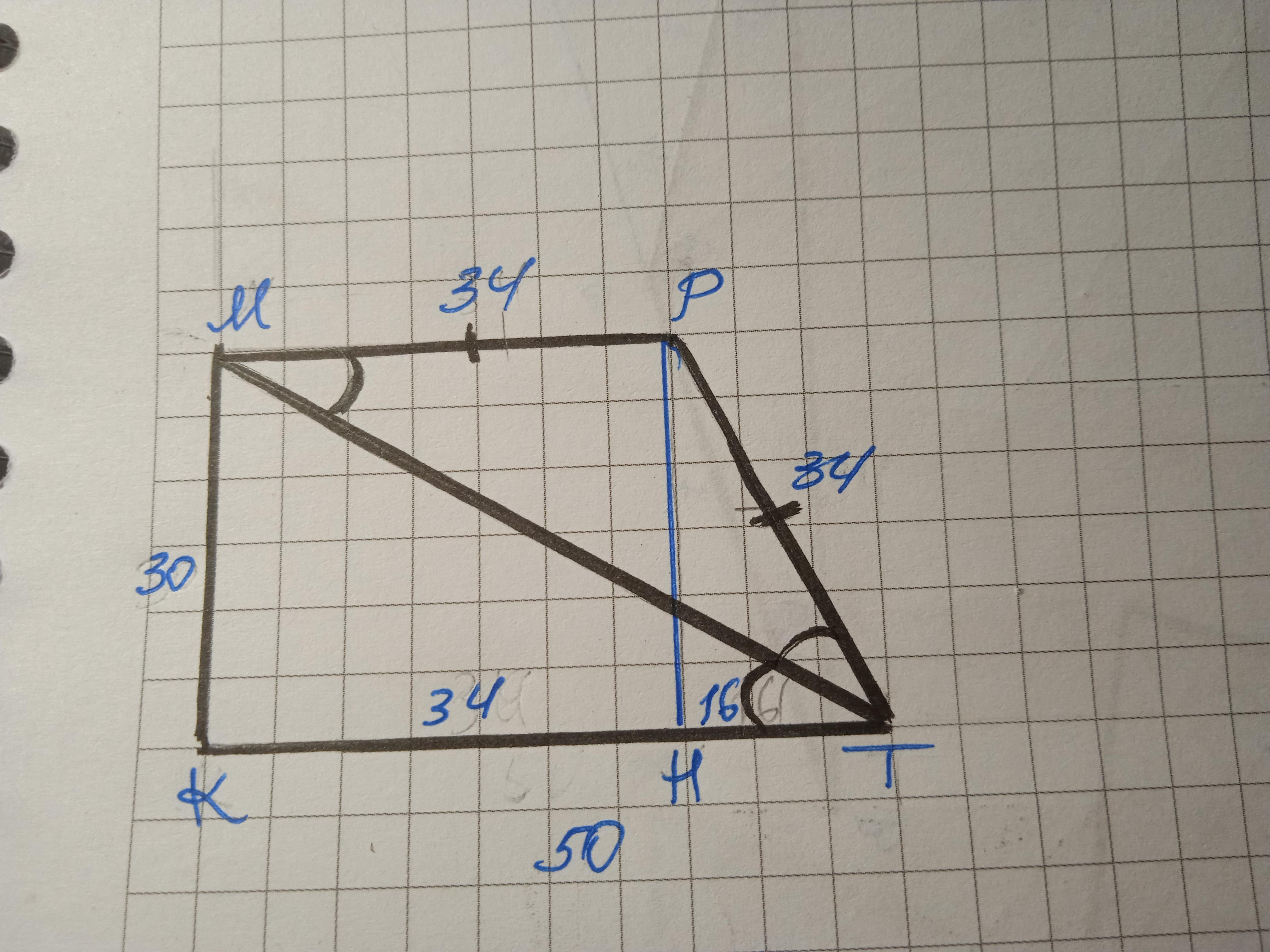
Дано: КМРТ - трапеция, МК⊥КТ, КТ=50 см, РТ=34 см. МТ - биссектриса. Найти периметр КМРТ.
Биссектриса острого угла трапеции отсекает от неё равнобедренный треугольник.
ΔМРТ - равнобедренный, МР=РТ=34 см.
Проведем высоту РН, ΔТРН - прямоугольный.
ТН=КТ-КН=50-34=16 см
По теореме Пифагора РН=МК=√(РТ²-ТН²)=√(1156-256)=√900= 30 см.
30+34+34+50=148 см - это периметр трапеции.