Question

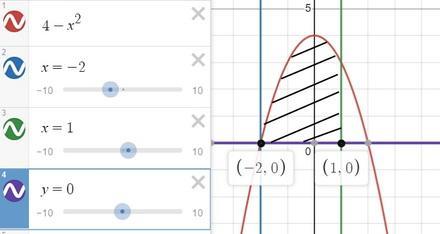
найдите площадь криволинейной трапеции,ограниченной осью ox, прямыми x=-2 и x=1 графиком функции y=4-x2

Answer 1

Ответ:

Пошаговое объяснение:

рисуем графики функций, определяем искомую трапецию, пределы интегрирования и подынтегральную функцию

$\displaystyle S= \int\limits^a_b {(y_1(x)-y_2(x))} \, dx$

у нас

a = 1

b = -2

за у₁ принимают функцию, график которой лежит "выше" на координатной плоскости. у нас это

у₁ = 4-х²

тогда

у₂ = 0 (это из условия ограниченной осью ox)

тогда наш интеграл

$\displaystyle S=\int\limits^1_{-2} {(4-x^2) } \, dx =4\int\limits^1_{-2} { } \, dx =-\int\limits^1_{-2} {(x^2) } \, dx =4x\bigg |_{-2}^1-\frac{x^3}{3} \bigg |_{-2}^1=12-3=9$