Предмет: Алгебра,
автор: KantemirMakhov
СОРЧНО! решите эти два уравнения, пожалуйста.
Приложения:
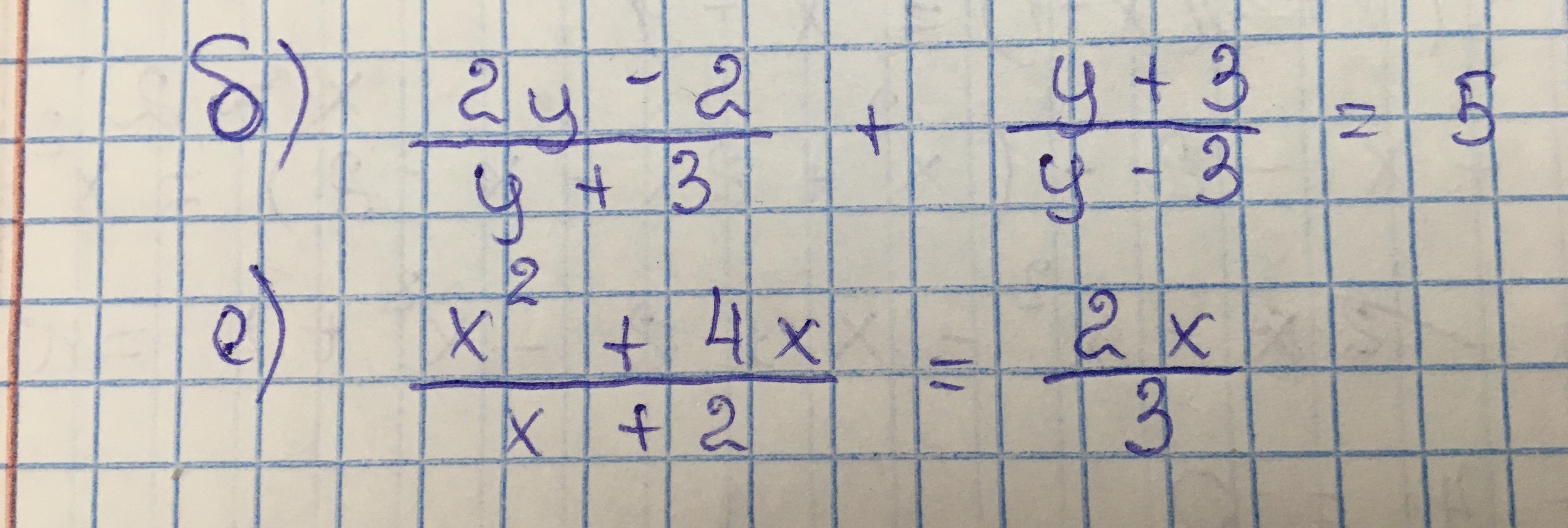
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: УченицаЭвилина
Предмет: Русский язык,
автор: vladbekish070
Предмет: Русский язык,
автор: Листики
Предмет: Геометрия,
автор: Plushtrap
Предмет: Математика,
автор: pyanoes