Предмет: Математика,
автор: nglushcov
Одна из диагоналей трапеции, которая равна 3√6 образует с основанием трапеции угол 60 градусив.Обчислиты длину второй диагонали, если она образует угол 45 градусов.
Ответы
Автор ответа:
0
Ответ: 9 .
Пошаговое объяснение:
ABCD - трапеція ; AC = 3√6 ; ∠CAD = 60° ; ∠ABD = 45° .Проведемо
BN⊥AD , CM⊥AD , тоді BN = CM = h - висота трапеції .
Із прямок. ΔАСМ : СМ = ACsin60° = 3√6 * √3/2 = 4,5√2 ; h = 4,5√2 .
Із прямок. ΔBND: BD = BN/sin45° = 4,5√2 /( √2/2 ) = 9 ; BD = 9.
nglushcov:
лучший, спасибо
Автор ответа:
0
Ответ:
9 од.
Пошаговое объяснение:
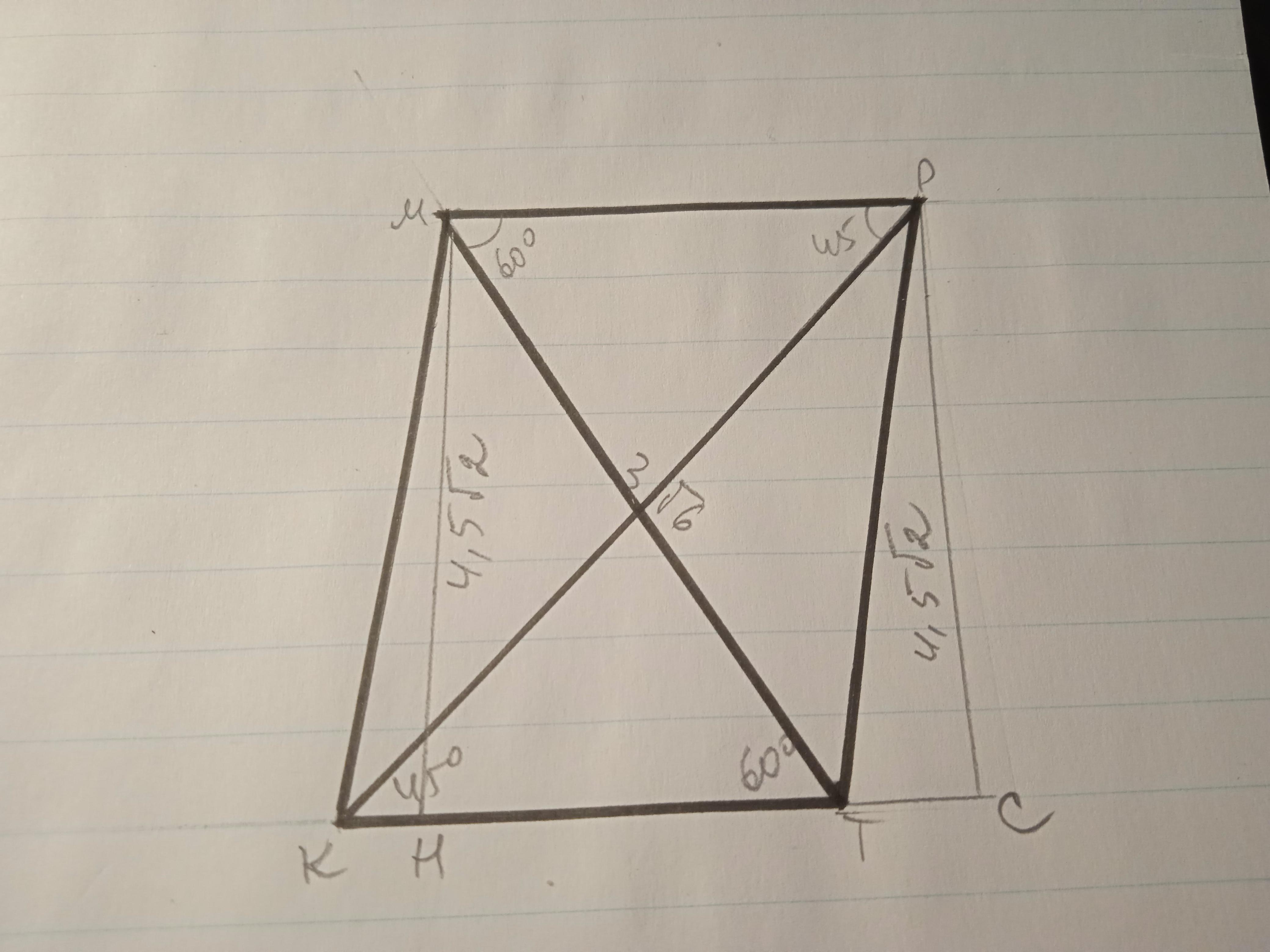
Дано: КМРТ - трапеція ; МТ = 3√6 ; ∠КТМ = 60° ; ∠РКТ = 45° . Знайти РК.
Проведемо МН і РС - висоти трапеції .
ΔМНТ; МН = МТ*sin60°=3√6 * √3/2 = 4,5√2 ;
ΔРСК; РК = РС/sin45° = 4,5√2/(√2/2 )=9 ; РК = 9.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: ЛиИЯЛИ
Предмет: Другие предметы,
автор: LaSSeRFeeD
Предмет: Русский язык,
автор: Аноним
Предмет: История,
автор: томирис63
Предмет: Математика,
автор: alinaalina12131