Предмет: Геометрия,
автор: hfhjuy
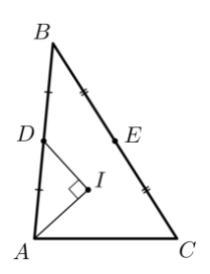
Точка I — центр окружности, вписанной в треугольник ABC, D — середина стороны AB. Найдите периметр треугольника, если известно, что AC=1, а угол AID прямой.
Приложения:
Ответы
Автор ответа:
3
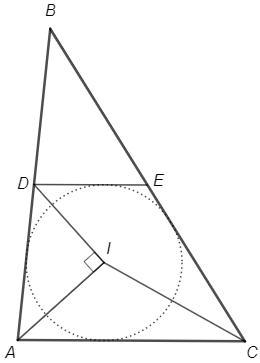
DE||AC, DE=AC/2 (средняя линия)
∠ADE+∠DAC=180 (внутренние углы при параллельных)
Пусть биссектрисы углов ADE и DAC пересекаются в точке X.
∠ADX+∠DAX =90 => ∠AXD=90
Из точки D можно опустить только один перпендикуляр к прямой AI =>
точки X и I совпадают => DI - биссектриса ∠ADE
В трапеции ADEC биссектрисы трех углов пересекаются в одной точке - трапеция описанная (т.е. имеет вписанную окружность).
В описанном четырехугольнике суммы противоположных сторон равны.
AD+CE =AC+DE
DE =AC/2 =0,5 => AC+DE =1,5 =AD+CE
AB+BC =2(AD+CE) =2*1,5 =3
P(ABC) =AB+BC+AC =3+1 =4
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Termin987
Предмет: Қазақ тiлi,
автор: maksim2329
Предмет: Русский язык,
автор: боловница
Предмет: Химия,
автор: viktoriyaaleks5
Предмет: Русский язык,
автор: Naruto2018