Предмет: Алгебра,
автор: kamilmatematik100504
Решите!!!!!!!!!!!!!!!!
Приложения:
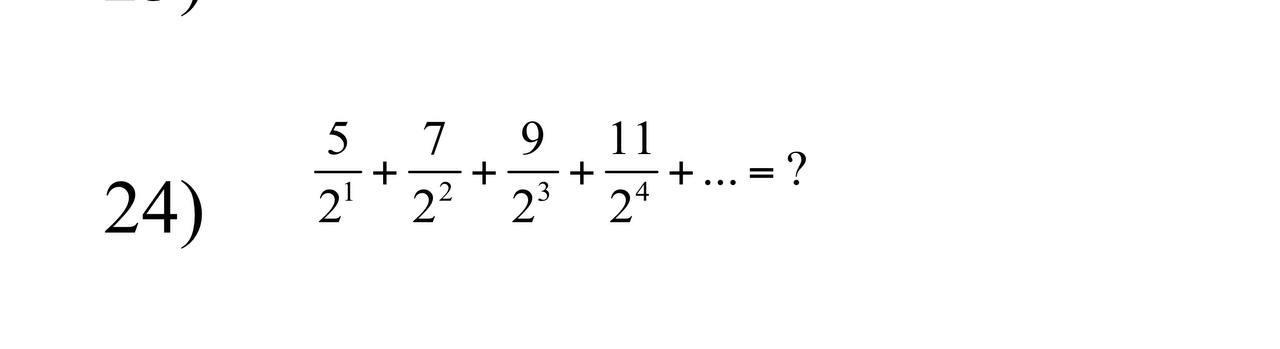
Ответы
Автор ответа:
4
Ответ:
Объяснение:
Найдем вспомогательную сумму .
, а значит ряд сходится, и
конечна.
Заметим:
Вернемся к исходному условию:
__________________________
Если применять идею сразу:
Пусть .
, а значит ряд сходится, и
конечна.
Заметим:
igorShap:
Кстати говоря, идею нахождения вспомогательной суммы можно было применить и сразу к исходному ряду, расписав его член как 1/2 * (2(k-1)+3)/2^(k-1)+1/2^(k-1)
Добавил этот вариант
Ну это бородатая задачка) Уже на так интересно
Это как я называю: арифметико-геометрическая прогрессия. Можно вывести не только для арифметической прогрессии в числителе, можно для последовательности квадратов, кубов и n- степеней в числителе
Похожие вопросы
Предмет: Другие предметы,
автор: Кристина628
Предмет: Технология,
автор: Бе3умныйНиК
Предмет: Русский язык,
автор: Karinozka
Предмет: Алгебра,
автор: FinnWolfhard1
Предмет: Українська мова,
автор: А2р3и1н8а9