Question

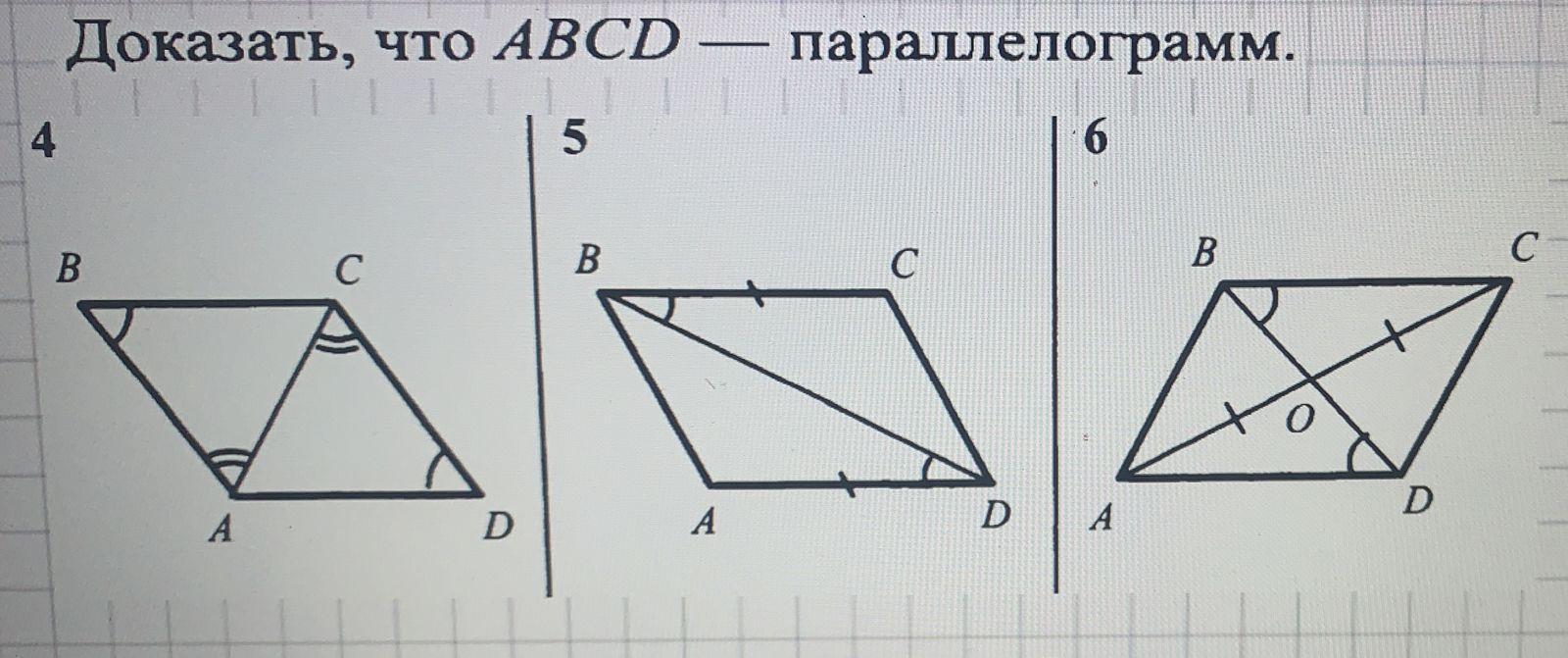
Доказать, что ABCD — параллелограмм
Помогите пожалуйста. (Только 6)

Answer 1

Объяснение:

1)

углы CBD и ADB равны

Один из признаков параллелограмма это паралельные противоположные стороны, углы CBD и ADB накрест лежащие углы , что доказывает параллельность сторон ВС и AD

2)

Четырёхугольник является параллелограммом, если его диагонали пересекаются и точкой пересечения делятся пополам.

диагональ BD делит диагональ АС пополам

что ещё раз доказывает что четырехугольник ABCD параллелограм

Answer 2

Объяснение:

Так как угол ∠СВО=∠АДВ как внутренние разносторонние, следовательно ВС || АД. Рассмотрим ∆ВОС и ∆АОД. Поскольку

ВС || АД, то ∠ВСО=∠ДАО, ∠ВОС=∠АОД как вертикальные, АО=СО – по условию, следовательно ∆ВОС=∆АОД по второму признаку, по стороне и прилежащим к ней углам. Тогда ВО=ДО и ВС=АД.

Рассмотрим ∆АОВ и ∆СОД, у них:

1) АО=СО

2) ВО=ДО

3) ∠АОВ=∠СОД, как вертикальные

Следовательно ∆АОВ=∆СОД, тогда АВ=СД.

Так как в четырёхугольнике АВСД АВ=СД, ВС=АД, ВО=ДО, АО=СО – противоположные стороны четырёхугольника АВСД равны, а также диагонали пересекаясь, делятся пополам, значит АВСД – параллелограмм

ДОКАЗАНО