Предмет: Алгебра,
автор: artEmPiv
Помогите пожалуйста!!!!!!
найдите сумму
Приложения:
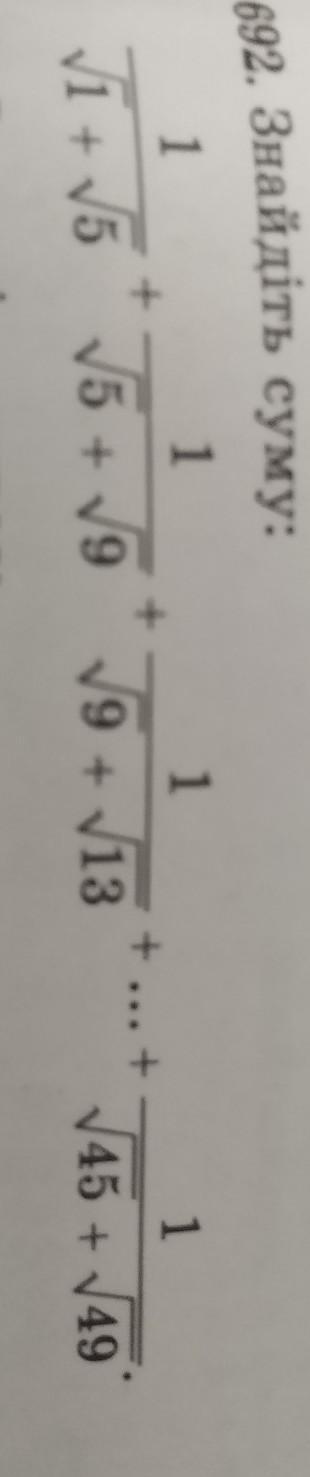
kamilmatematik100504:
12
в книжке написано 1,5
Ответы
Автор ответа:
2
Ответ:
1,5
объяснение в фотографии
Приложения:

Автор ответа:
4
Ответ:
1.5
Объяснение:
Используем разность квадратов: (a-b)(a+b)=a²-b²
При этом: (√a-√b)(√a+√b)=(√a)²-(√b)²=a-b
Похожие вопросы
Предмет: Қазақ тiлi,
автор: марина123544
Предмет: Русский язык,
автор: Nikita228007
Предмет: Русский язык,
автор: линова250
Предмет: Алгебра,
автор: vikavikamiros
Предмет: Математика,
автор: nikitos230