Предмет: Геометрия,
автор: yamamurasadako20
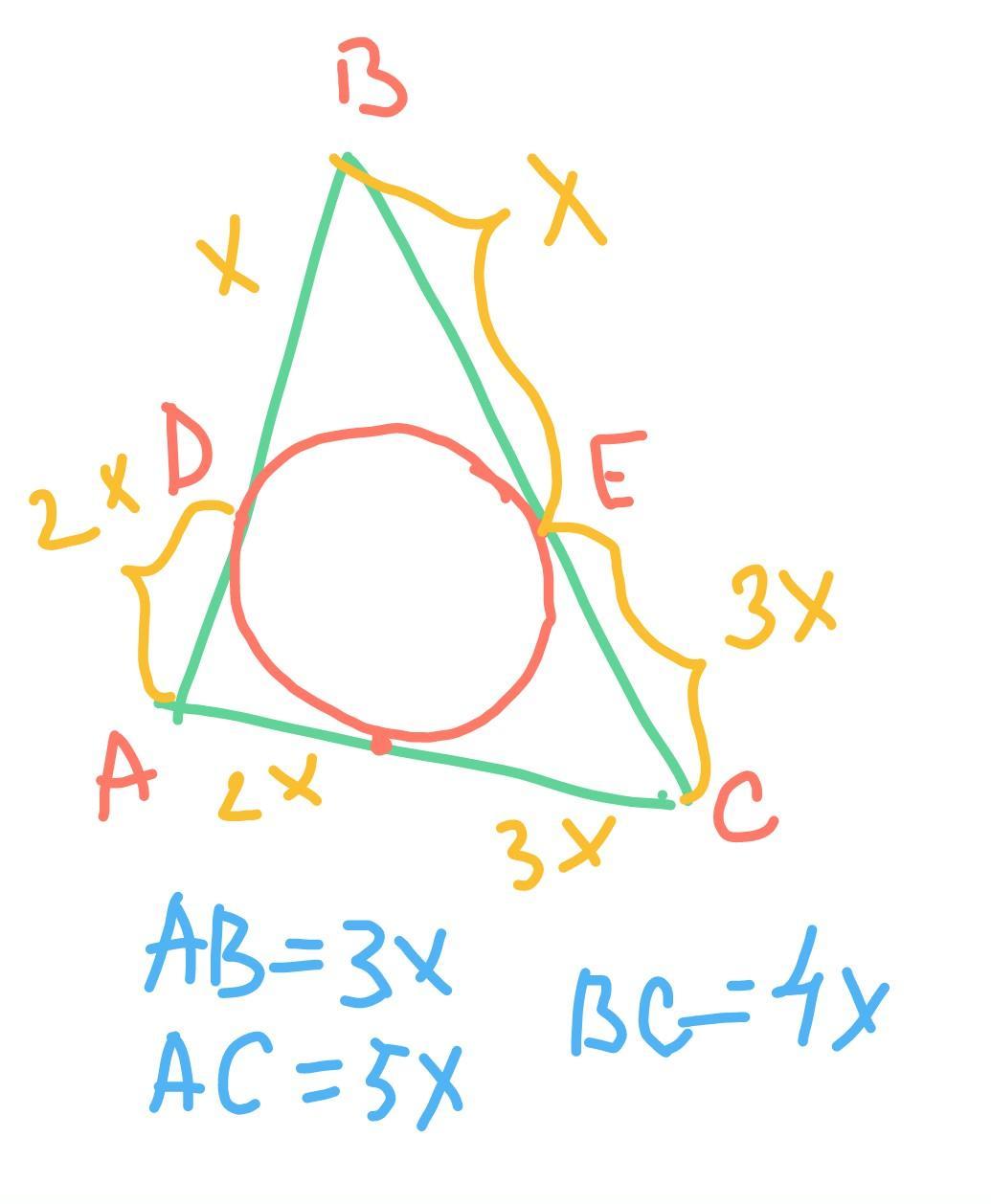
1.В треугольнике АВС вписана окружность, касающаяся стороны АВ в точке D и стороны ВС в точке Е.Найти углы треугольника, если ВD : АD= 1 : 2, ВЕ : СЕ = 1 : 3.
2. В прямоугольном треугольнике катеты равны AC=12 см и BC=16 см. Вычислить: 1) периметр ; 2) площадь; 3)радиус вписанной окружности ; радиус описанной окружности; 5) sin A , cos B, tg A, ctg B.
Ответы
Автор ответа:
1
Ответ:
B=90° A=60° C=30°
P=50см,S=112см² sinA=0,8, tgA=4/3 , cosB=0,8 , ctgB=4/3
Объяснение:
(1)AB:BC:AC=3:4:5
если соотношение между сторонами треугольника равны 3:4:5 , то треугольник прямоугольный, а его углы составляют 90°,60° и 30°
сторона АС самый длинный, соответственно угол противоположный стороне АС равен 90°
угол В=90°
сторона ВС>АВ
значит противоположный угол в стороне ВС 60°
угол А=60°
а угол С =30°
(2)
1)чтобы найти периметр , найдем гипотенузу треугольника
АВ²=АС²+ВС² =144+256=400
АВ=20
Р=14+16+20=50
Р=50см
2)
S=1/2×AC×BC=1/2×14×16=112см²
S=112см²
3)
sinA=BC/AB=16/20=0,8
thA=BC/AC=16/12=4/3
cosB=CB/AB=16/20=0,8
ctgB=BC/AC=16/12=4/3
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: позитив007
Предмет: Беларуская мова,
автор: 090620061
Предмет: Русский язык,
автор: wwwmaruska2009
Предмет: Геометрия,
автор: littlecrybaby
Предмет: Математика,
автор: peoplepersonpeo