Предмет: Геометрия,
автор: annakir7
В треугольнике абс угол а = 45°. Серединный перпендикулюр к стороне аб пересекает ас в точке д. Докажите, что вс>сд
Ответы
Автор ответа:
3
Ответ:
доказано
Объяснение:
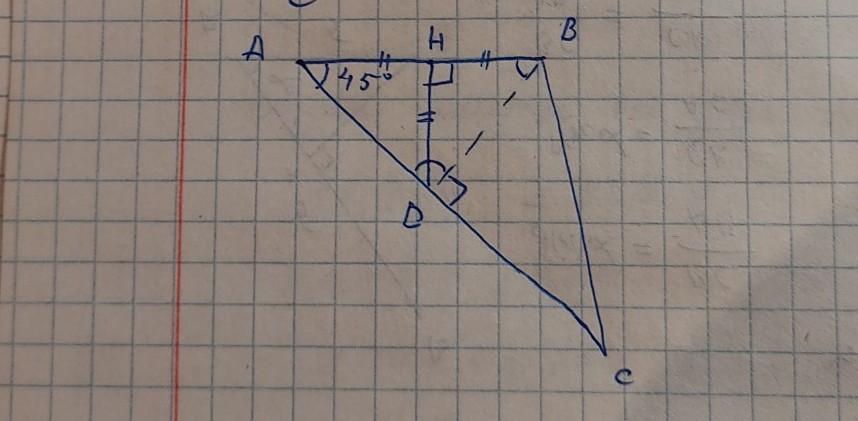
нарисуем треугольник АВС
где угол А =45°и нарисуем серединную высоты к стороне АВ
АН=НВ=НD потому что прямоугольный треугольник АНD равнобедренный
проведём линию DB
линия DB перпендикулярна к стороне DC , потому что углы ADH и HDB по 45°,что значит угол BDC 180°-45°-45°= 90°
из этого выходит что треугольник BDC прямоугольный
сторона ВС является гипотенузой этого треугольника , сторона DC катетом
в прямоугольном треугольнике гипотенуза всегда длиннее катетов , это значит ВС>CD
доказано
Приложения:
cdcsac:
спасибо большое за "лучший ответ")
Похожие вопросы
Предмет: Русский язык,
автор: андрей853
Предмет: Английский язык,
автор: aniasatryan20
Предмет: Русский язык,
автор: olgavaimer72
Предмет: Математика,
автор: tvaylaytcet
Предмет: Психология,
автор: vvodka777