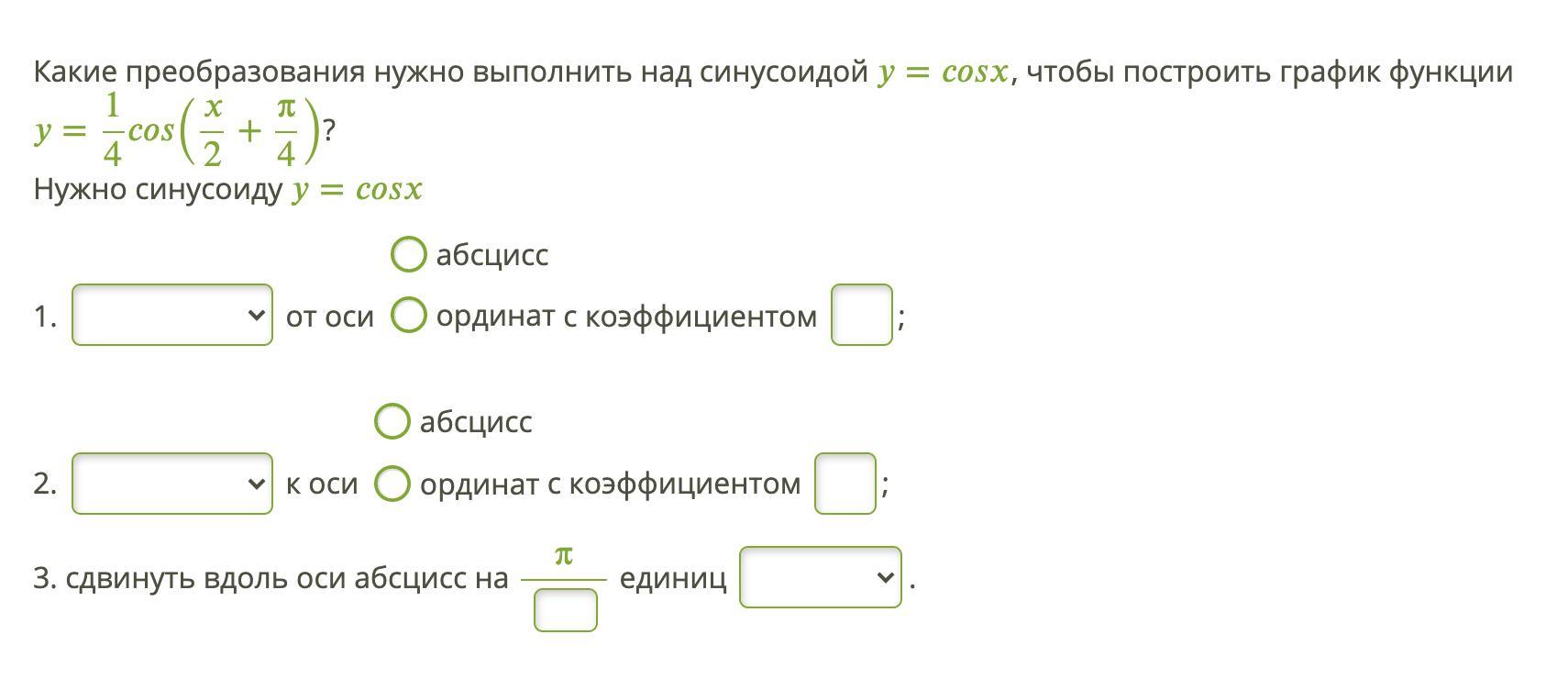
Какие преобразования нужно выполнить над синусоидой y=cosx, чтобы построить график функции
Ответы
Ответ:
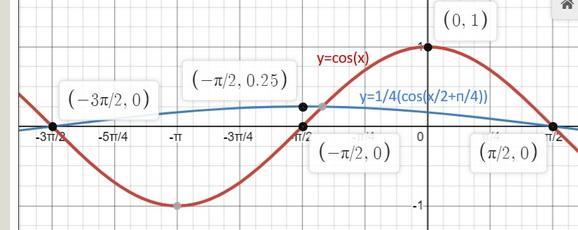
1) функцию y=cos(x) сжать по оси ОY (к оси ОХ) в 4 раза
2) функцию y=cos(x) растянуть по оси ОХ (от оси OY) в 2 раза
3)нужно функцию y=cos(x) сдвинуть по оси ОХ на
(на влево)
Объяснение:
из всех правил сдвига графика функций, я выберу те, которые касаются нашей функции
1. если ФУНКЦИЯ умножается на число 1/m ( m >1) , то происходит сжатие её графика вдоль оси ОY в m раз
2. если АРГУМЕНТ функции умножается на 1/k (k>1) , то график функции растягивается вдоль оси ОХ в к раз
3. если к АРГУМЕНТУ функции добавляется константа b y(x+b), то происходит сдвиг (параллельный перенос) графика вдоль оси ОХ на b единиц влево (на -b единиц) .
Теперь проделаем все это с нашей функцией
начнем с простого
1. у нас ФУНКЦИЯ умножается на число 1/4, значит мы будем сжимать функцию y = cos(x) в 4 раза вдоль оси OY
2. у нас АРГУМЕНТ функции умножается на 1/2, значит мы будем растягивать график у = cos(x) по оси ОХ в 2 раза
3. а вот теперь тут будет не так просто. поскольку правило 3 справедливо для графика функции y(x+b), нам надо привести свою заданную функцию к такому виду
таким образом у нас будет сдвиг (параллельный перенос) графика
у = cos(x) вдоль оси OX на единиц влево
Ну и вот что должно получиться.
#SPJ3