Предмет: Математика,
автор: katyastri51
Вопрос: какой тут ответ?
Приложения:
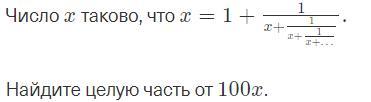
Ответы
Автор ответа:
1
Пусть ;так как данная дробь периодическая и бесконечна, то для неё верно:
(*). Далее перепишем исходное уравнение в виде: х = 1 + А; подставляя это в (*), получим:
⇒
⇒
A(1+2A) = 1 ⇒ 2A² + A - 1 = 0, откуда А = - 1 или А = 0,5. Второе значение положительно, оно и будет подходящим значением дроби .
Тогда А = 0,5 и х = 1 + 0,5 = 1,5 ⇒ 100х = 100·1,5 = 150 ⇒ [100x] = 150
Ответ: целая часть от 100х равна 150
Похожие вопросы
Предмет: Русский язык,
автор: ромка23
Предмет: Окружающий мир,
автор: barys82
Предмет: Английский язык,
автор: мария958
Предмет: Математика,
автор: arinkaarinka3
Предмет: Алгебра,
автор: Макс78963585