Предмет: Математика,
автор: lunnaiapoxodka6
А. Для углов a,b,y в треугольнике докажите:
Приложения:
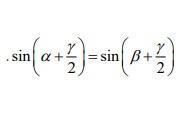
Ответы
Автор ответа:
1
Пошаговое объяснение:
Так как - углы треугольника,
.
Значит, .
Но тогда, т.к. , получим
.
Ч.т.д.
lunnaiapoxodka6:
а почему одна звезда? кто-то считает решение неверным?
Автор ответа:
1
Решение:
cos 0.5γ · (sin α - sin β) + sin 0.5γ · (cos α - cos β) = 0
cos 0.5γ · 2 cos 0.5(α + β) · sin 0.5(α - β) -
-sin 0.5γ · 2 sin 0.5(α + β) · sin 0.5(α - β) = 0
2 sin0,5(α - β) · (cos 0.5γ · cos 0.5(α + β) - sin 0.5γ · sin 0.5(α + β) ) = 0
2 sin0,5(α - β) · (0.5(cos0.5 (α + β + γ) + cos0.5(γ - α - β)) +
+ 0.5(cos0.5 (α + β + γ) - cos0.5(γ - α - β) )) = 0
2 sin0.5(α - β) · 0.5cos0.5 (α + β + γ) (0.5cos0.5(γ - α - β) -
- 0.5cos0.5(γ - α - β) ) =0
α + β + γ = 180° ⇒ cos0.5 (α + β + γ) = cos 90° = 0
sin(α - β) · 0 · 0 = 0
0 ≡ 0
Тождество доказано.
Похожие вопросы
Предмет: Русский язык,
автор: stmisynovagali
Предмет: Русский язык,
автор: яна612
Предмет: Русский язык,
автор: enigma1954
Предмет: Русский язык,
автор: Шуся14
Предмет: История,
автор: эльмира168