Предмет: Математика,
автор: yanabond54
8. Решите уравнение

ответе укажите наименьший положительный корень уравнения. Ответ:24
Ответы
Автор ответа:
0
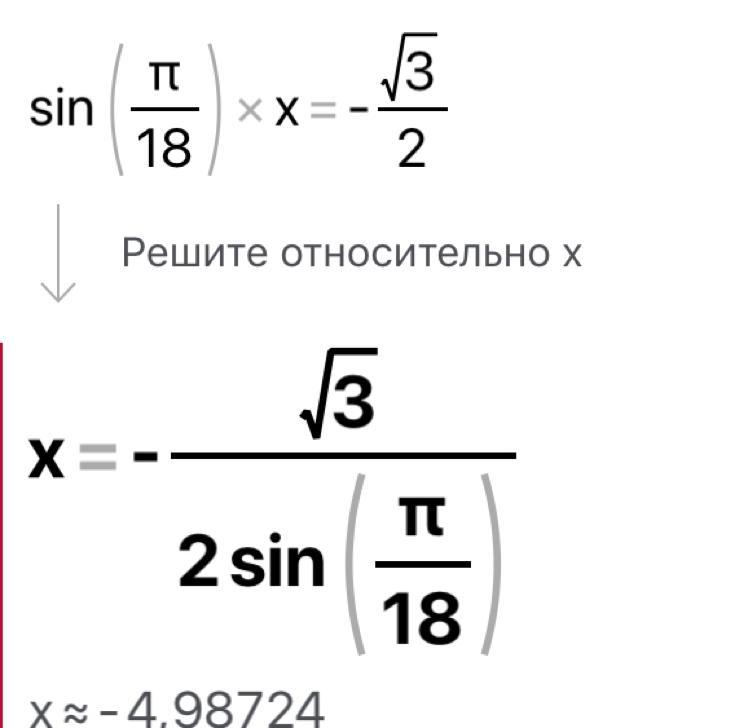
Вот ответ! Я сокращённо сделала, могу подробно
Приложения:
Автор ответа:
1
Ответ:
24
Пошаговое объяснение:
Чтобы получился показанный ответ нужно небольшое изменение условия. Вместо
должно быть
Похожие вопросы
Предмет: Русский язык,
автор: alfiya1978
Предмет: Русский язык,
автор: swerell
Предмет: Русский язык,
автор: Данюшкин
Предмет: Русский язык,
автор: mad123man5
Предмет: Математика,
автор: gperchiny