ниже скрин................
Ответы
Ответ:
Объяснение:
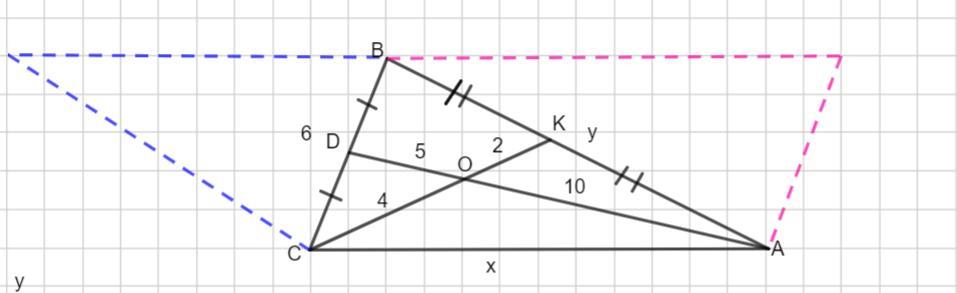
В треугольнике АВС проведены медианы AD=15, CK=6.
Медианы пересекаются в точке О и точкой пересечения делятся в отношении 2 к 1, считая от вершины.
Тогда АО=10, ОD=5 и СО=4, ОК=2.
Определим какая сторона может быть равна 6.
Рассмотрим Δ АОС . Сторона АС не может быть равна 6, так как нарушается неравенство треугольника( сторона АО= АС+СО).
Если сторона АВ=6, то АК=ВК = 3 .Рассмотрим ΔАОК: АО> OK+AK Неравенство треугольника тоже нарушается и сторона АВ не может быть равна 6.
Значит, ВС=6.
Пусть АС= x , АВ= y.
Достроим до параллелограмма и воспользуемся свойством квадратов диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Cоставим и решим систему уравнений .
Условию задачи удовлетворяют только положительные значения.
Значит,