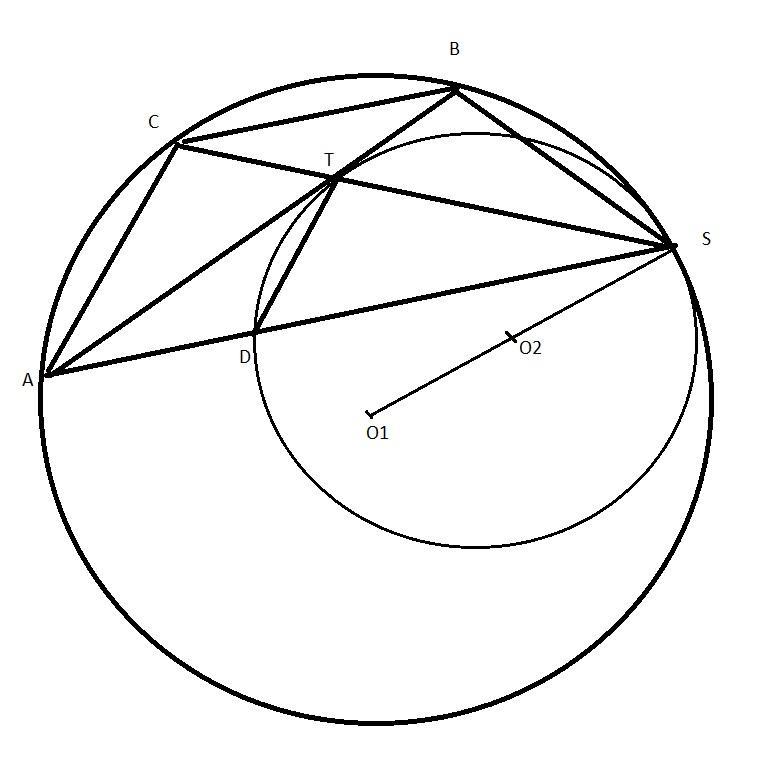
Две окружности касаются внутренним образом в точке S. Хорда AB внешней окружности касается внутренней окружности в точке T. Прямая ST пересекает внешнюю окружность в точках S и C. Найдите площадь четырёхугольника SABC, если известно, что CA=5, CB параллельна AS, а радиусы окружностей относятся как 11:16.
Ответы
По лемме Архимеда: BST = CSA , тогда AB и CS биссектрисы углов CAS и BSA соответственно, по условию BS || AS и AB касательная к меньшей окружности, тогда TSD = ATD = CAB то есть TD || AC.
ABCS равнобедренная трапеция и AC=BC=BS = 5. (опираются на одни и те же вписанные углы)
Пусть O1 , O2 центры большей и меньших окружностей и r1, r2 их радиусы соответственно, очевидно что O1,O2,S лежат на одной прямой, из-за параллельности TD || AC то есть CAS = TDS получается CO1S = TO2S = 2*CAS , то есть треугольники TO2S , CO1S подобны, откуда ST/SC = SO2/SO1 = r2/r1 = 11/16
SC/ST = 16/11
CT/ST = 5/11
так как AT биссектриса, то по теореме о биссектрисе AC/AS = CT/ST=5/11
AC=5, AS=11
получаем равнобедренную трапецию ABCS все стороны известны
опустим высоту AH из вершины C на AS, которая равна h, тогда AH=(11-5)/2=3
CH=√(5^2-3^2) = 4
S(ABCS) = (5+11)*4/2 = 32