Предмет: Математика,
автор: ksumaylz
Стороны прямоугольника заданы уравнениями 3x+4y+1=0 (ab) 2x-y-3=0 (bc) x+5y-7=0 (ac) составьте уравнение высоты ad. сделайте чертеж
Ответы
Автор ответа:
0
Ответ:
x+2y-7=0
Пошаговое объяснение:
AB∩AC=A
3x+4y+1=0 (AB)
x+5y-7=0 (AC)
x=7-5y
3(7-5y)+4y+1=0
21-15y+4y+1=0
22-11y=0
11y=22
y=2
x=7-5y=7-10=-3
A(-3; 2)
AD⊥BC
Уравнение прямой проходящей через точку M(x₀; y₀) и перпендикулярной прямой заданной уравнением ax+by+c=0, представляется уравнением a(y-y₀)-b(x-x₀)=0
Уравнение прямой проходящей через точку A(-3; 2) и перпендикулярной прямой заданной уравнением 2x-y-3=0, представляется уравнением 2(y-2)-(-1)(x-(-3))=0
2y-4+x-3=0
x+2y-7=0
Приложения:
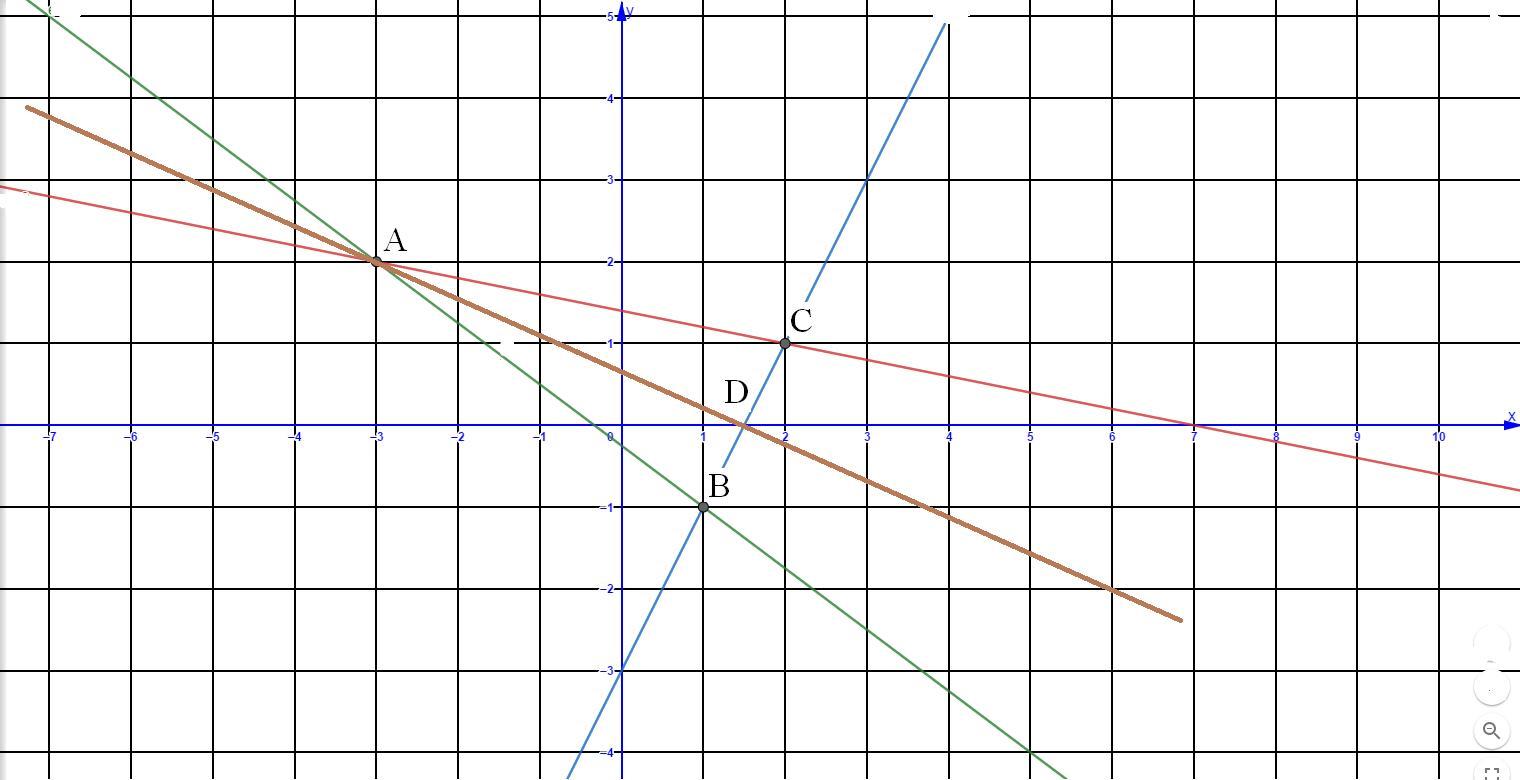
Автор ответа:
0
Ответ:
Приложения:
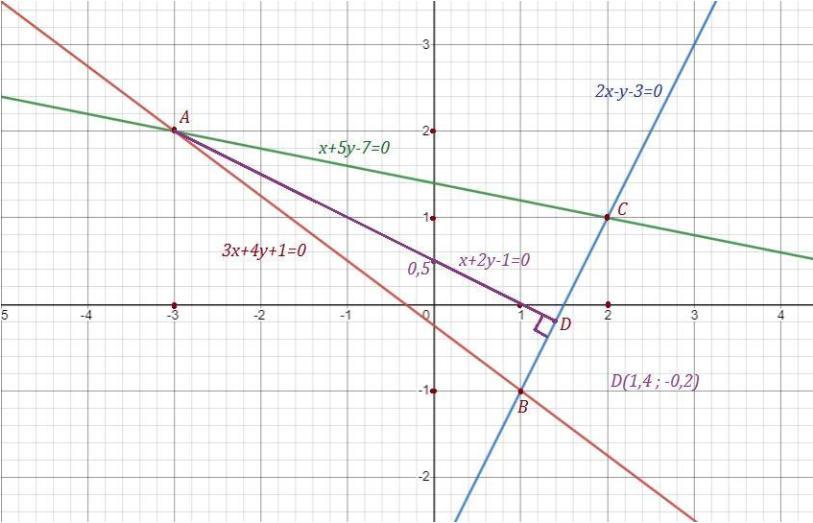
Похожие вопросы
Предмет: Українська мова,
автор: ZNIKE
Предмет: Окружающий мир,
автор: mashaMedved1
Предмет: Українська мова,
автор: salimonovrus
Предмет: Математика,
автор: sergey212kor2
Предмет: Биология,
автор: madinakoroeva