Стереометрия. Найти углы между прямыми
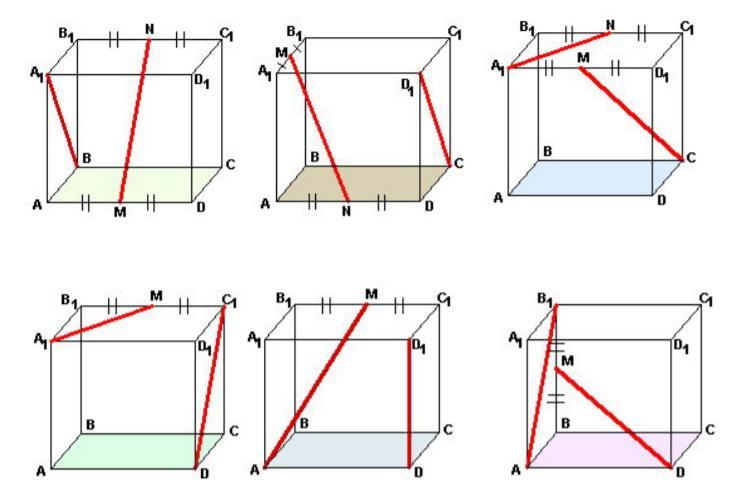
Ответы
Ответ:
Объяснение:
По корректировке автора в коментах ABCDA₁B₁C₁D₁-куб.
Введу обозначение. (AB)-вектор AB.
Расположим данные кубы в системе координат, единичный отрезок равен ребру куба.
Точка B-начало координат, A∈Ox, C∈Oy, B₁∈Oz
Будем находить углы используя формулу для угла между векторами.
Учитывая, что при α>90° переходим к углу 180°-α
A(1; 0; 0), B(0; 0; 0); C(0; 1; 0); D(1; 1; 0), A₁(1; 0; 1), B₁(0; 0; 1); C₁(0; 1; 1); D₁(1; 1; 1)
Показанные координаты точек во все шести заданиях неизменны.
Будем только находить координаты точек M и N. Во всех заданиях данные точки(если они присутствуют) являются серединами рёбер. Будем использовать для нахождения их координат известную формулу середины отрезка:
M∈AB, AM=BM, A(a;b;c), B(d;e;f), M(x;y;z)⇒x=(a+d)/2; y=(b+e)/2; z=(c+f)/2
1) M∈AD, AM=DM, A(1; 0; 0), D(1; 1; 0)⇒M(1; 0,5; 0)
N∈B₁C₁, B₁N=C₁N, B₁(0; 0; 1); C₁(0; 1; 1)⇒N(0; 0,5; 1)
(BA₁)={1;0;1}; (MN)={-1; 0; 1}
(BA₁)·(MN)=1·(-1)+0·0+1·1=0⇒(BA₁)⊥(MN)⇒BA₁^MN=(BA₁)^(MN)=90°
Можно было решить другим способом. Достроим AB₁.
BA₁⊥AB₁⇒BA₁^AB₁=90°
B₁N=0,5B₁C₁=0,5AD=AM; B₁N║AM⇒AB₁NM-параллелограмм ⇒MN║AB₁⇒MN^BA₁=BA₁^AB₁=90°
Но будем придерживаться 1-го способа.
2) M∈A₁B₁, A₁M=B₁M, A₁(1; 0; 1), B₁(0; 0; 1)⇒M(0,5; 0; 1)
N∈AD, AN=DN, A(1; 0; 0), D(1; 1; 0)⇒N(1; 0,5; 0)
(CD₁)={1;0;1}; (NM)={-0,5; -0,5; 1}
|CD₁|=√(1²+0²+1²)=√2; |NM|=√((-0,5)²+(-0,5)²+1²)=√1,5
(CD₁)·(NM)=1·(-0,5)+0·(-0,5)+1·1=0,5
cos((CD₁)^(NM))=(CD₁)·(NM)/(|CD₁|·|NM|)=0,5/(√2√1,5)=√3/6
⇒CD₁^NM=(CD₁)^(NM)=arccos(√3/6)
Дальше всё так же