Предмет: Алгебра,
автор: artemsuvorov2
a,b- неотрицательные числа. Докажите неравенство
Приложения:
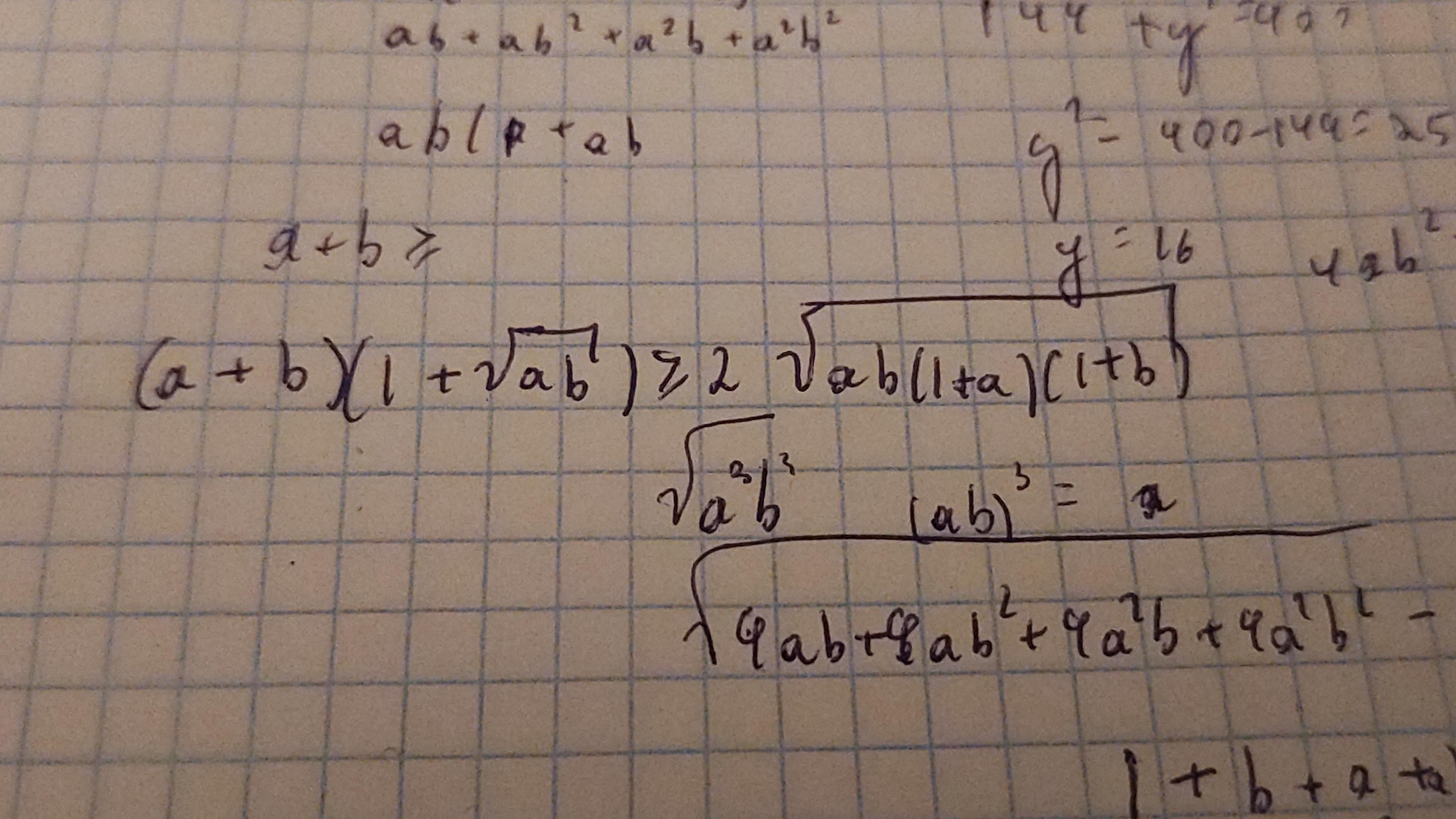
Ответы
Автор ответа:
0
Раскроем слева скобки: (по нер-ву между ср. а и ср. г). Далее то же неравенство:
Похожие вопросы
Предмет: Русский язык,
автор: аквамарин51
Предмет: Английский язык,
автор: lanamara
Предмет: Русский язык,
автор: 123456789523
Предмет: Информатика,
автор: тьютььь1
Предмет: Химия,
автор: Аноним