Предмет: Геометрия,
автор: aanonimovic06
Кут при основі AB рівнобедреного трикутника дорівнює 30 градусів. Висоти трикутника, проведені до бічних сторін, перетинаються в точці O. Знайти у градусах величину кута AOB.
Ответы
Автор ответа:
4
Відповідь:
60°.
Пояснення:
Кути при основі по 30°, тому кут при вершині ACB дорівнює 180°-30°-30°=120°. Нехай AL - висота до сторони CB, а BK - до сторони AC. Тому розглянемо чотирикутник CKOL, у ньому кути OKC та OKL по 90°, кут KCL - 120°. Тому кут KOL дорівнюватиме 360°-90°-90°-120°=60°. Тоді кут AOB теж 60°, тому що KOL та AOB - вертикальні кути.
Приложения:
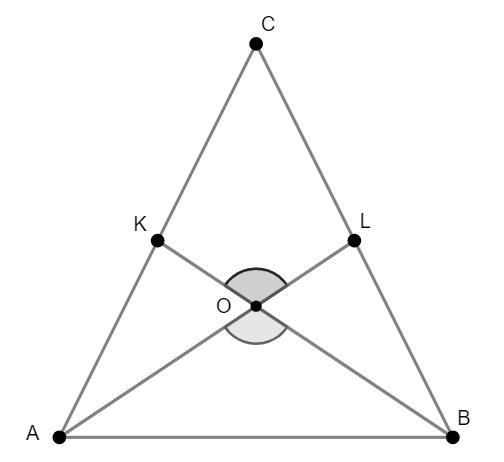
Пеппер:
рисунок не соответствует условию задачи
Автор ответа:
4
Ответ:
60°
Объяснение:
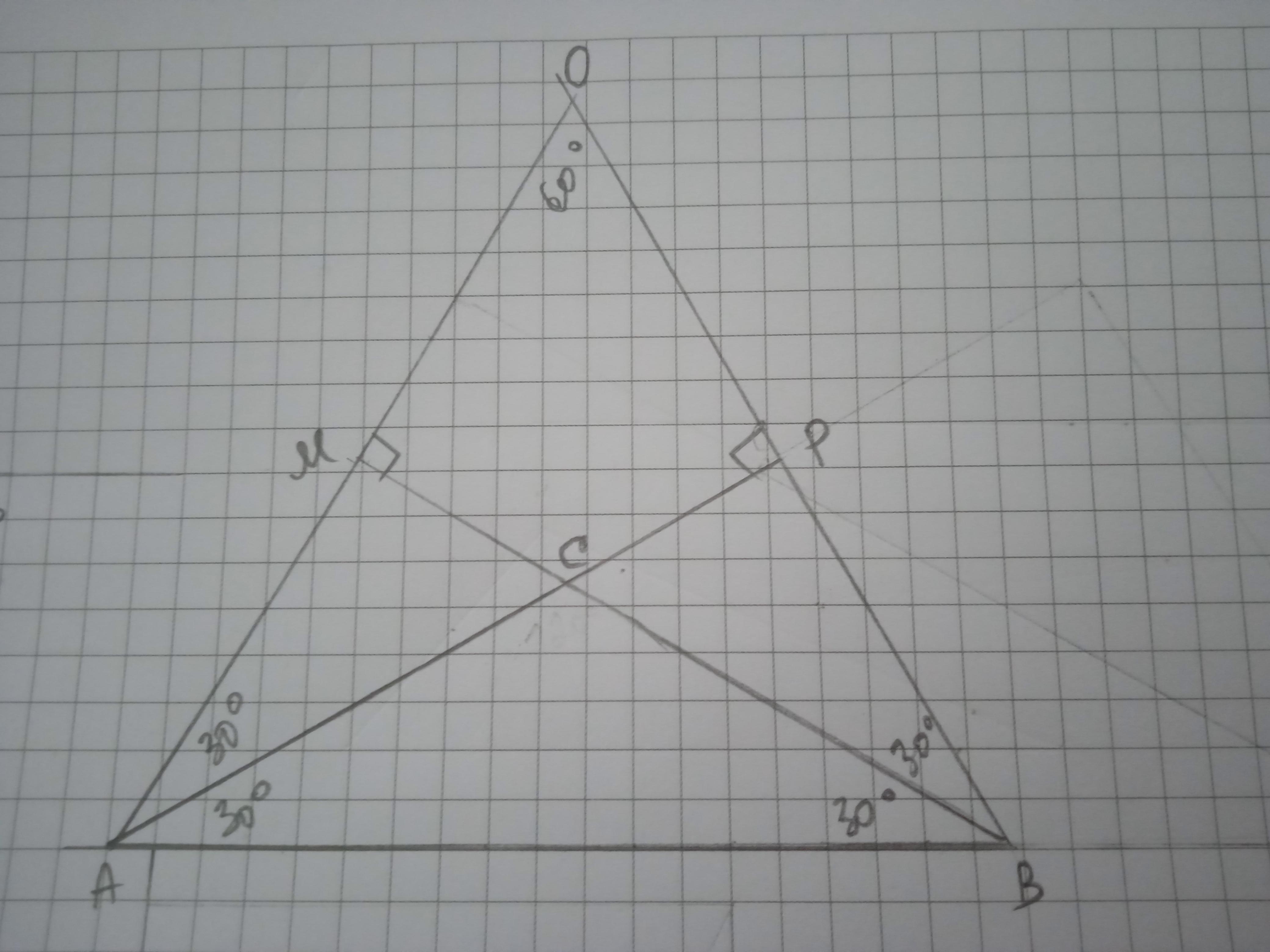
ΔАВС - тупокутний, ∠С=180-30-30=120°, тому висоти припадають на продовження його бокових сторін.
Проведемо висоти АР та ВМ, які перетинаються у точці О.
Розглянемо ΔАВМ та ΔАРВ. ΔАВМ = ΔАРВ (АВ - спільна сторона, АР=ВМ як висоти, проведені до бічних сторін рівнобедреного трикутника, ∠АМВ=∠АРВ). Отже ∠МАВ=∠АВР=90-30=60°.
ΔАОВ - рівнобедрений, ∠А=∠В=60°, ∠АОВ=180-60-60=60°
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Mi5lPog1ariФ
Предмет: Русский язык,
автор: njuvikyskaDIA
Предмет: Окружающий мир,
автор: rom252
Предмет: Химия,
автор: Kessv
Предмет: Алгебра,
автор: долтг