Решите уравнение : .........................
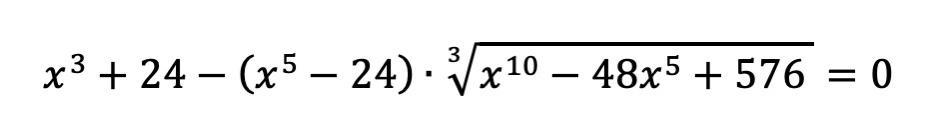
Ответы
Сначала приведем стандартное доказательство равносильности уравнений
f(f(x))=x и f(x)=x, если известно дополнительно, что f(x) - монотонно возрастающая функция (на самом деле доказательство проходит и в случае уравнений f(f(f(...(f(x))...)))=x и f(x)=x).
Если то
то есть все решения второго решения являются решениями первого.
Если то
В самом деле, если
(или
), то
(или соответственно
). В этом месте доказательства мы и использовали монотонное возрастание функции. Поэтому все решения первого уравнения являются решениями второго. Итак, равносильность уравнений доказана.
Переходим к конкретному уравнению. Преобразуем его:
Если рассмотреть функцию то уравнение может быть записано в виде f(f(x))=x, а поскольку функция f(x) монотонно возрастающая, уравнение равносильно уравнению f(x)=x, то есть
Чтобы было проще в дальнейшем, докажем, что это уравнение не имеет отрицательных корней. В самом деле, если x∈[-1;0], то "побеждает" 24. Иными словами, левая часть отрицательна, корней на этом отрезке быть не может. Если x∈(-∞;-1), то
и поэтому
Далее: угадываем корень x=2( искали естественно среди делителей свободного члена), делим многочлен на x-2 и получаем уравнение
которое не может иметь положительных корней в силу положительности всех коэффициентов, и не может иметь отрицательных корней, так как иначе исходное уравнение имело бы отрицательные корни, а мы доказали, что их нет.
Ответ: 2