Предмет: Математика,
автор: Аноним
Сколько положительных решений имеет уравнение:
(x^2+6x)^4 + 8(x^2+6x)^2-9=0
Приложения:
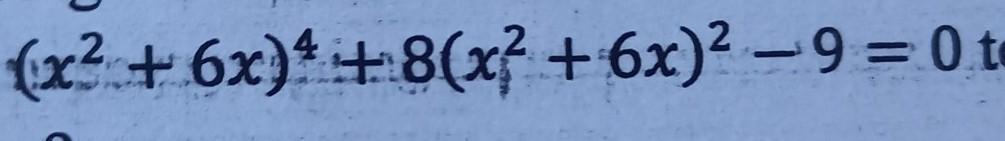
Viva8888:
x^2 + 6x = t
t^4 + 8t^2 - 9 = 0
a = t^2
лучше (x^2 + 6x)^2 = t
t1 = -9 посторонний корень t2 = 1
Ответы
Автор ответа:
0
Пошаговое объяснение:
Пусть (х²+6х)²=t≥0 ⇒
Так как: х₁=-3-√10≈-6,16
х₂=-3+√10≈0,16
х₃=-3-2√2≈-5,83
х₄=-3+2√2≈-0,17, а по условию задачи x>0 ⇒
Ответ: x=-3+√10.
На вопрос: Сколько положительных решений имеет уравнение. Ответ: одно решение х2.
Sailcar100, спасибо за уточнение. Действительно: Ответ: x=-3+√10.
Увлёкся решением, забыл про условие! Это мой прокол.
Просьба к модератору - предоставьте возможность на исправление ответа данной задачи.
Похожие вопросы
Предмет: Русский язык,
автор: лерочка40
Предмет: Русский язык,
автор: sasha1shabanova
Предмет: Английский язык,
автор: vasilkova333
Предмет: Русский язык,
автор: AZAZAden62
Предмет: Алгебра,
автор: зкд3