Какие утверждения верны?
а) Высота прямоугольного треугольника с углом 60°, проведённая к гипотенузе, равна половине большего катета этого треугольника.
б) Если периметры двух прямо- угольников равны, то и сами прямоугольники равны.
в) Если боковая сторона и угол при основании одного равнобедренного треугольника соответственно равны боковой стороне и углу при основании другого равнобедренного треугольника, то такие треугольники равны.
г) Медиана треугольника не может совпадать с его биссектрисой.
объясните пожалуйста
Ответы
Ответ:
а) Высота прямоугольного треугольника с углом 60°, проведённая к гипотенузе, равна половине большего катета этого треугольника.
Верно!
б) Если периметры двух прямоугольников равны, то и сами прямоугольники равны.
Неверно!
в) Если боковая сторона и угол при основании одного равнобедренного треугольника соответственно равны боковой стороне и углу при основании другого равнобедренного треугольника, то такие треугольники равны.
Верно!
г) Медиана треугольника не может совпадать с его биссектрисой.
Неверно!
Пошаговое объяснение:
Определить, какие утверждения верны.
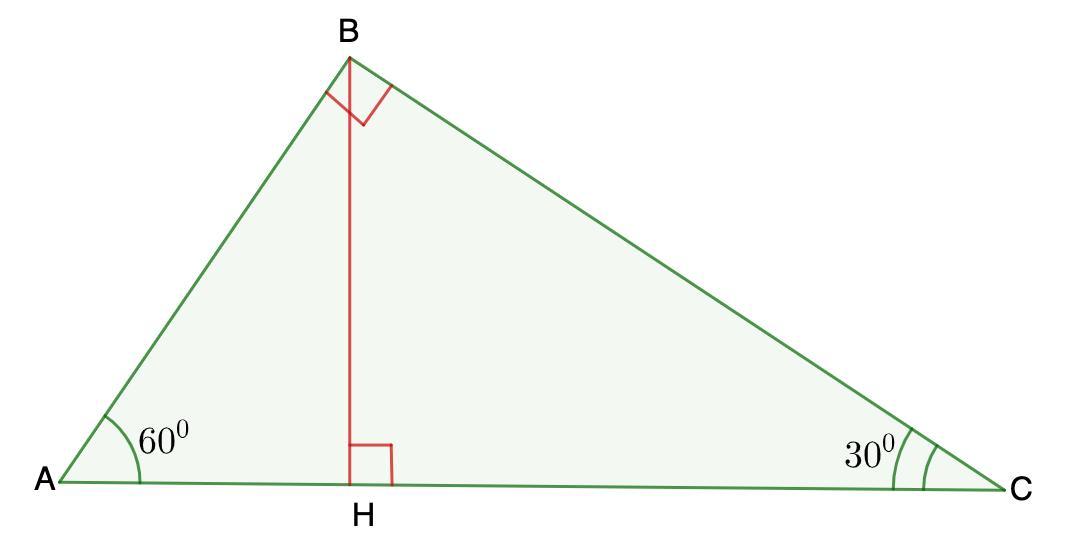
а) Высота прямоугольного треугольника с углом 60°, проведённая к гипотенузе, равна половине большего катета этого треугольника.
Рассмотрим ΔАВС - прямоугольный.
∠А = 60°
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠С = 90° - 60° = 30°
Рассмотрим ΔНВС - прямоугольный.
∠С = 30°
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒ ВН = 0,5 ВС
То есть, высота прямоугольного треугольника с углом 60°, проведённая к гипотенузе, равна половине большего катета этого треугольника.
Верно!
б) Если периметры двух прямоугольников равны, то и сами прямоугольники равны.
- Два прямоугольника считаются равными, если у них равны две стороны при одной вершине (длина и ширина).
Предположим, что периметры данных прямоугольников 12 см.
- Периметр прямоугольника равен удвоенной сумме длины и ширины.
Р = 2(a + b)
12 = 2 (a + b)
или
6 = a + b
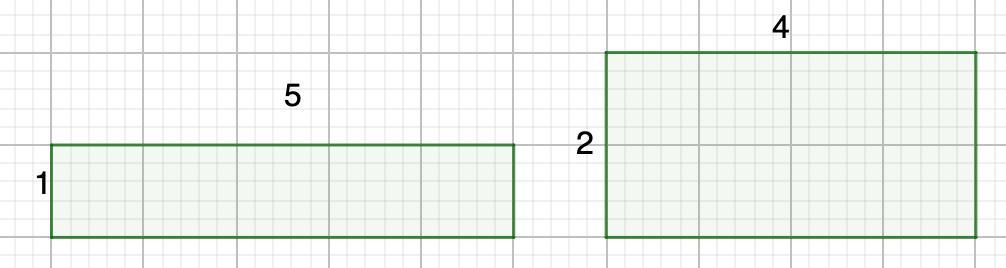
Видим, что в данном случае возможны варианты:
a = 1; b = 5
a = 2; b = 4
То есть, прямоугольники с одинаковыми периметрами не обязательно равны.
Неверно!
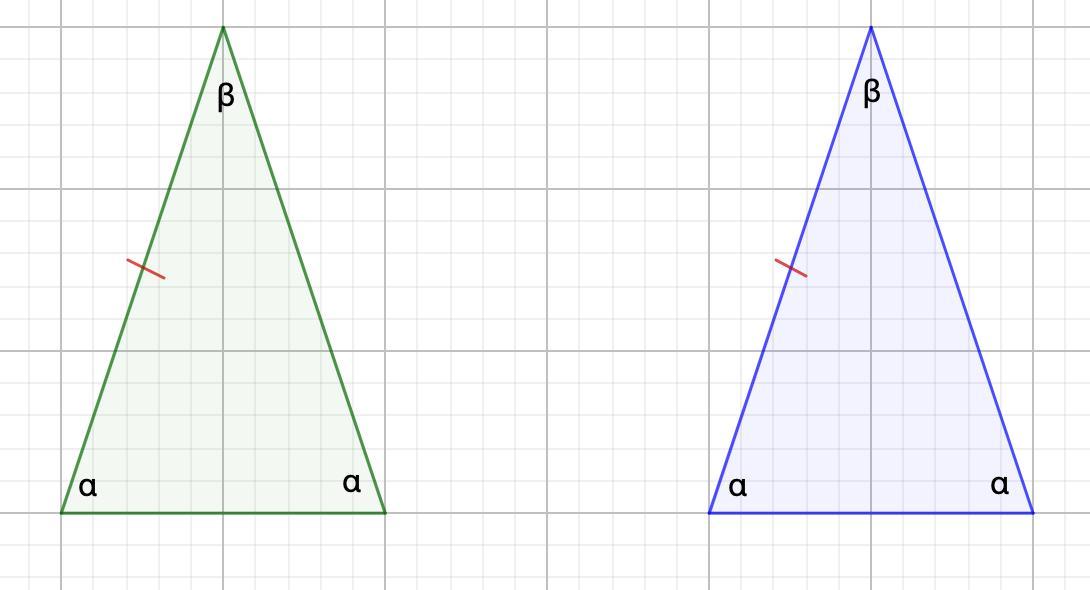
в) Если боковая сторона и угол при основании одного равнобедренного треугольника соответственно равны боковой стороне и углу при основании другого равнобедренного треугольника, то такие треугольники равны.
Действительно, если принять один угол при основании за α, то другой угол будет равен α, так как
- Углы при основании равнобедренного треугольника равны.
- Сумма углов треугольника равна 180°.
Примем угол при вершине за β.
⇒ в каждом из треугольников
β = 180° - 2α
Следовательно треугольники будут равны по 2 признаку (по стороне и двум прилежащим к ней углам)
Верно!
г) Медиана треугольника не может совпадать с его биссектрисой.
Вспомним:
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
Неверно!