Question

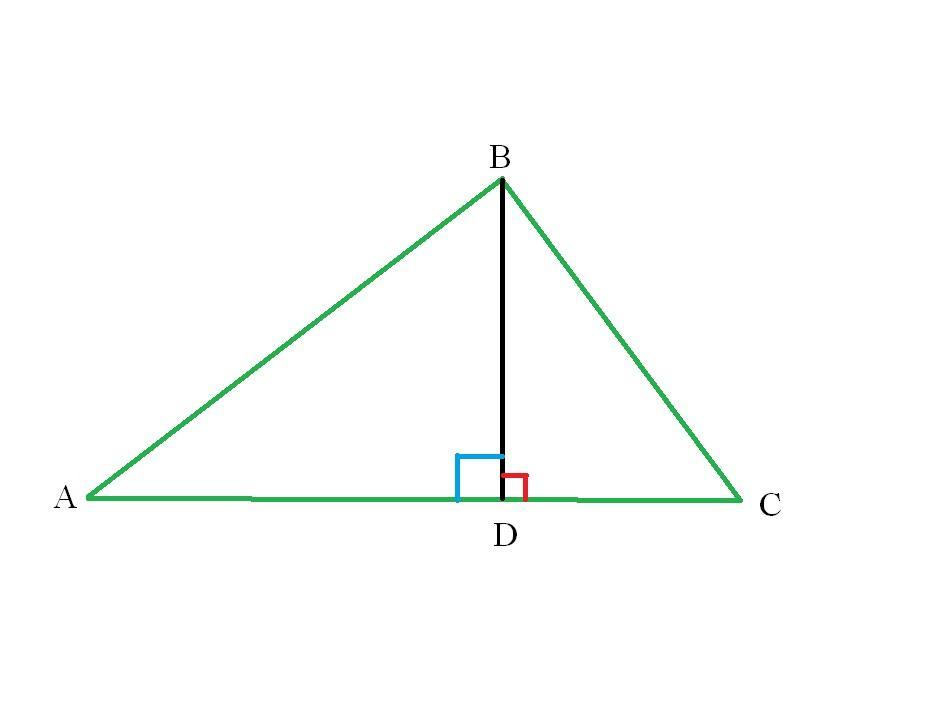
Высота BD треугольника ABC делит сторону AC на 3 и 7 равных отрезков. Найдите тангенс угла B, если BD = 4

Ответ на задачу -8 но как её решить хз, бьюсь который час

Answer 1

Ответ:

tg B = - 8

Объяснение:

Дано:

ΔАВС: BD  - высота

AD = 3

CD = 7

BD = 4

Найти:

tg B

Решение:

По теореме Пифагора

АВ² = BD² + AD²

АВ² = 4² + 3²

AB² = 25

Тоже по теореме Пифагора

ВС² = BD² + CD²

ВС² = 4² + 7²

BC² = 65

По теореме косинусов

АС² = АВ² + ВС² - 2 · АВ · ВС · cos B

Откуда

$cos~B = \dfrac{AB^2 + BC^2- AC^2}{2\cdot AB\cdot BC} = \dfrac{25 + 65- 10^2}{2\cdot 5\cdot \sqrt{65} } = -\dfrac{1}{\sqrt{65} }$

Площадь треугольника АВС

S = 0.5 · AC · BD = 0.5 · 10 · 4 = 20

C другой стороны площадь треугольника АВС

S = 0.5 · AB · BC · sin B

Откуда

$sin~B = \dfrac{2\cdot S}{AB \cdot BC} = \dfrac{2\cdot 20}{5 \cdot \sqrt{65} } = \dfrac{8}{\sqrt{65} }$

И, наконец,

$tg~B = \dfrac{sin~B}{cos~B} = \dfrac{8\cdot \sqrt{65} }{(-1)\cdot \sqrt{65} } =-8$

Answer 2

Ответ:

-8

Объяснение:

Изменённое условие. Высота BD треугольника ABC делит сторону AC на отрезки равные 3 и 7 . Найдите тангенс угла B, если BD = 4.

AD=7, CD=3, BD=4, ∠BDC=∠BDA=90°, ∠ABD=α, ∠CBD=β, ∠B=α+β

$tg\alpha =\frac{AD}{BD}=\frac{7}{4}\\tg\beta =\frac{CD}{BD}=\frac{3}{4}\\tgB=tg(\alpha +\beta )=\frac{tg\alpha+tg\beta}{1-tg\alpha*tg\beta}\\tgB=\frac{\frac{7}{4}+\frac{3}{4} }{1-\frac{7}{4}*\frac{3}{4}}=\frac{\frac{5}{2} }{1-\frac{21}{16}}=\frac{\frac{5}{2} }{-\frac{5}{16}}=-\frac{5}{2}*\frac{16}{5}=-8$