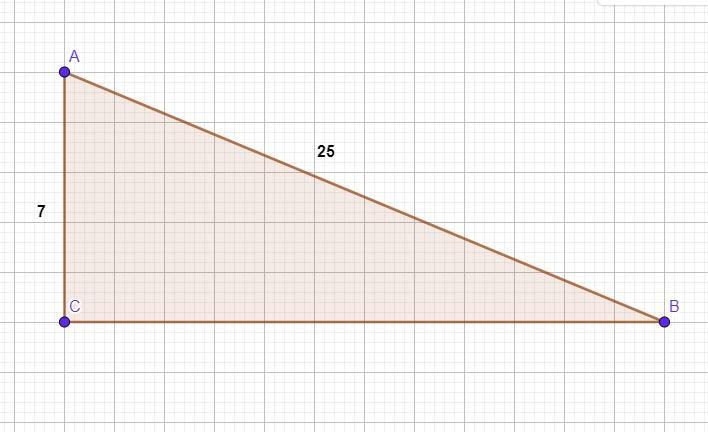
катет и гипотенуза прямоугольного треугольника соответственно равняются 7 и 25 см.Найдите синус угла, противолежащий большому катету. 2) косинус угла,противолежащий большему катету.3) тангенс угла, прилежащий к меньшему катету
Ответы
Ответ:
1) sin ∠A = 0,96
2) cos ∠A = 0,28
3) tg ∠A ≈ 3,43
Объяснение:
В прямоугольном треугольнике АВС катет АС = 7 см, а гипотенуза АВ = 25 см. Надо найти:
1) синус угла, противолежащий большому катету.
2) косинус угла, противолежащий большему катету.
3) тангенс угла, прилежащий к меньшему катету
- Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе.
- Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.
- Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.
РЕШЕНИЕ
Для начала найдём неизвестный катет прямоугольного ΔАВС по теореме Пифагора:
ВС²=АВ²-АС²=25²-7²=625-49=576
ВС=√576= 24 см
1) Найдём синус угла, противолежащий большому катету.
Так как ВС> AC, то ВС - больший катет ΔАВС. ∠А - угол, противолежащий ВС
sin∠A = BC/AB =24/25= 0,96
2) косинус угла, противолежащий большему катету.
cos∠A = AC/AB = 7/25 = 0,28
3) тангенс угла, прилежащий к меньшему катету.
АС - меньший катет ΔАВС. ∠А - угол, прилежащий к катету АС.
tg∠A = BC/AC = 24/7 ≈ 3,43
#SPJ3