Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить!!!
Приложения:
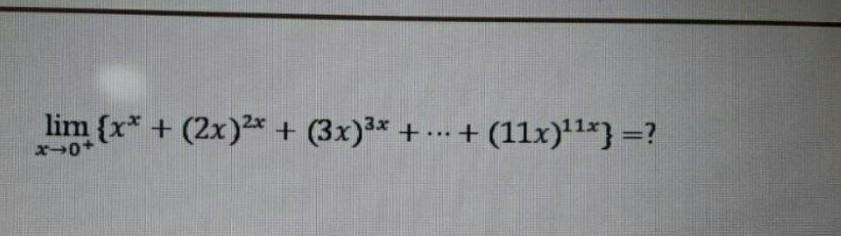
Alexandr130398:
фигурные скобки что то значат?
ну тогда 11 должно получиться
Ответы
Автор ответа:
1
Ответ:
11
Объяснение:
Докажем в общем виде, что
Пусть y=(nx)ⁿˣ, тогда найдем следующий предел:
значит
- ч.т.д.
Похожие вопросы
Предмет: Русский язык,
автор: ммммм16
Предмет: Английский язык,
автор: YaroslavRazuva
Предмет: Русский язык,
автор: diana197676
Предмет: Математика,
автор: ladylandish