Предмет: Геометрия, автор: matveymat71

В остроугольном равнобедренном треугольнике ABC с равными сторонами AB и BC
окружность, проходящая через точку пересечения высот из вершины B и C, пересекает
сторону AB в точке D.
-------------------------------------
Нарисуйте пожалуйста рисунок к задаче, заранее спасибо!

sailcar100: Про центр окружности ничего не сказано? А то вариантов чертежа много может быть.

matveymat71: Нет к сожалению. Все что дано это это условие и еще пункт а и б а) Доказать, что треугольники ABC и ACD подобны.
б) Найти косинусы углов треугольника ABC, если известно, что D–середина AB.

dosmtv: варианта чертежа 2

cos20093: Ну, можно "раскрутить" загадку с конца. В каком случае ABC и ACD подобны? Это дает точное расположение точки D на AB - она симметрична A относительно высоты из вершины C. Кроме того, из подобия следует ∠HBD=∠HCD H - точка пересечения высот. => окружность проходит через A, D, H и B. Вот что должно быть в условии. Только в этом случае ABC и ACD подобны.

dosmtv: это какой класс?

matveymat71: 11 класс ЕГЭ По математике 16 задание. Предлагайте еще чертежи

siestarjoki: https://i.imgur.com/PUasYBm.png

Ответы

Автор ответа: owlsun709305

Объяснение:

наверное так. не уверена в условии в задании

Приложения:

Автор ответа: siestarjoki

----------------------------------------------

Приложения:

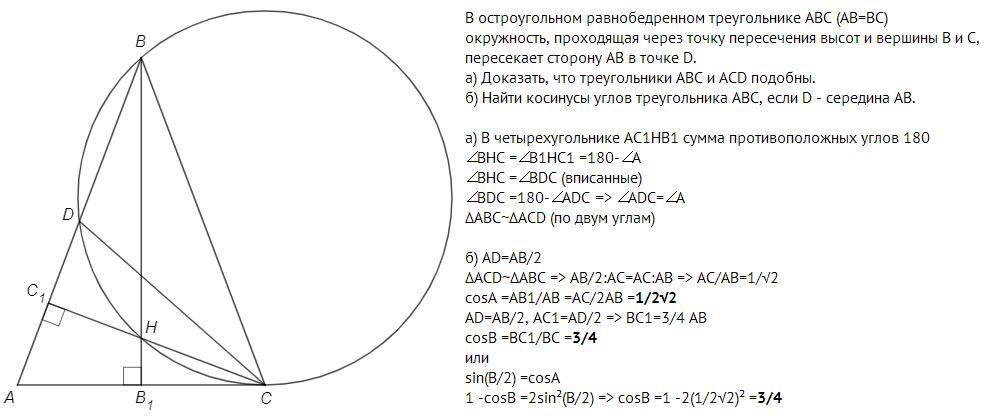
cos20093: Ну, тут важно, что точка D может находиться только в таком месте, что ∠ABC=∠ACD; при любом другом положении треугольники ABC и ACD не будут подобны. Скорее всего в тексте условия надо читать "и вершины B и C" а не "из", как автор решения и написал.

siestarjoki: конечно

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Русский язык, автор: gitlerdasha

проверочное слово к слову богатырей

2 года назад

Предмет: Английский язык, автор: vladayartseva

поставить предложения в отрицательную форму
1) Commercial loan is money that banks lend to businesses.
2) My friend has had a charge card.
3) It is necessary to check your credit file.
4) He borrows money to buy a house.
5) They lent money to him last year.

2 года назад

Предмет: Русский язык, автор: OlyaKruglikova

Пожалуйста помогите составить план на это сочинение...
Роман "Капитанская дочка" повествует о драматических событиях 70-х годов 18 века, когда недовольство крестьян и жителей окраин России вылилось в войну под предводительством Емельяна Пугачева. Первоначально Пушкин хотел написать роман, посвященный только пугачевскому движению, но цензура навряд ли пропустила бы его. Поэтому основной сюжетной линией становится любовь молодого дворянина Петра Гринева к дочери капитана Белогорской крепости Маше Мироновой.

В "Капитанской дочке" одновременно развивается несколько сюжетных линий. Одна из них-история любви Петра Гринева и Маши Мироновой. Эта любовная линия продолжается на всем протяжении романа. Сначала Петр отнесся к Маше отрицательно из-за того, что Швабрин описал ее "совершенною дурочкою". Но затем Петр знакомится с ней ближе и обнаруживает, что она "благородна и чувствительна". Он влюбляется в нее, и она тоже отвечает ему взаимностью.

Гринев очень сильно любит Машу и ради нее готов на многое. Он доказывает это не один раз. Когда Швабрин унижает Машу, Гринев ссорится с ним и даже стреляется. Когда перед Петром стоит выбор: подчиниться решению генерала и остаться в осажденном городе или откликнуться на отчаянный крик Маши "вы один у меня покровитель, заступитесь за меня, бедную! ", Гринев уезжает из Оренбурга, чтобы спасти ее. Во время суда, рискуя жизнью, он не считает возможным назвать имя Маши, боясь, что она будет подвергнута унизительному допросу-"мне пришло в голову, что если я назову ее, то комиссия потребует ее к ответу; и мысль впутать ее между гнусными изветами злодеев и ее самую привести на очную ставку... ".

Но и любовь Маши к Гриневу глубока и лишена каких-либо эгоистических побуждений. Она не хочет выходить за него замуж без родительского согласия, думая, что в противном случае у Петра "не будет счастия".Из робкой "трусихи" она, по воле обстоятельств, перерождается в решительную и стойкую героиню, сумевшую добиться торжества справедливости. Она едет ко двору императрицы, чтобы спасти своего возлюбленного, отстоять свое право на счастье. Маша смогла доказать невиновность Гринева, в ерность его данной присяге. Когда Швабрин ранит Гринева Маша выхаживает его-"Марья Ивановна от меня не отходила". Таким образом Маша спасет Гринева от позора, гибели и ссылки так же, как он спас ее от позора и гибели.

Для Петра Гринева и Маши Мироновой все заканчивается благополучно, и мы видим, что никакие превратности судьбы никогда не смогут сломить человека, если он настроен бороться за свои принципы, идеалы, любовь. Беспринципного и бесчестного человека, которому неведома чувство долга, часто ожидает участь остаться наедине со своими гадкими поступками, низостью, подлостью, без друзей, любимых и просто близких людей.