Предмет: Алгебра,
автор: nikitaalhimyonok
решите уравнение 1167
Приложения:
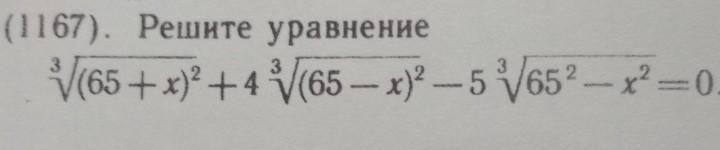
antonovm:
однородное относительно корней , 0 и 63
а поподробнее...
и почему не 0 и 65?
Ирина , молодые щас ответят , преподам надо вообще запретить решать
подождем)))
∛(65 + x) = a
∛(65 - x) = b
a^2 + 4b^2 - 5ba = 0
D = 25b^2 - 16b^2 = 9b^2
a12 = (5b +- 3b)/2 = 4b и b
∛(65 - x) = b
a^2 + 4b^2 - 5ba = 0
D = 25b^2 - 16b^2 = 9b^2
a12 = (5b +- 3b)/2 = 4b и b
Ответы
Автор ответа:
2
Ответ:
(см. объяснение)
Объяснение:
Уравнение однородное.
Тогда, поделив его на , перейдем к равносильной записи:
Введем замену вида .
Получим:
Обратная замена:
Значит и
являются корнями исходного уравнения.
Задание выполнено!
Похожие вопросы
Предмет: Русский язык,
автор: Мага20041
Предмет: Русский язык,
автор: ученица121
Предмет: Русский язык,
автор: zaharova14
Предмет: Химия,
автор: Nirlando
Предмет: Математика,
автор: Nailya11111