Предмет: Алгебра,
автор: Аноним
Вычислить сумму ряда
Приложения:
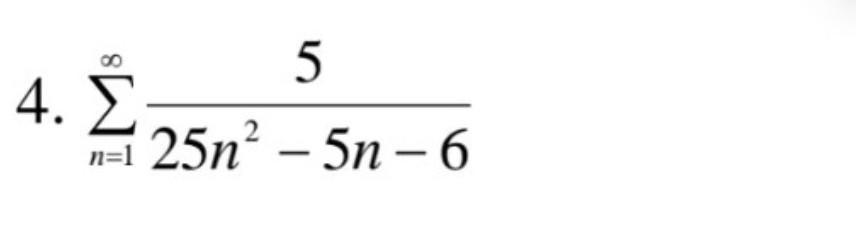
Ответы
Автор ответа:
3
Ответ:
1/2
Объяснение:
Попробуем разложить знаменатель на множители:
25n^2 - 5n - 6 = 0
D = 25 - 4*25*(-6) = 25 + 600 = 625 = 25^2
n1 = (5 - 25)/50 = -20/50 = -2/5
n2 = (5 + 25)/50 = 30/50 = 3/5
25n^2 - 5n - 6 = (5n + 2)(5n - 3)
Предположим, что дробь является суммой дробей:
Вычислим А и В:
Знаменатели равны, значит, числители тоже равны. Система:
{ A + B = 0
{ 2B - 3A = 5
Решаем подстановкой:
{ A = -B
{ 2B + 3B = 5
B = 1, A = -1
Получили такую разность:
Подставляем эту разность в нашу формулу ряда:
Все дроби после 1/2 сокращаются, и это продолжается бесконечно. Поэтому от всего ряда остается только первый член: 1/2
Удачник66:
Большое пожалуйста!
Похожие вопросы
Предмет: Русский язык,
автор: 1111192
Предмет: Английский язык,
автор: asusxptvasus
Предмет: Русский язык,
автор: 1231392
Предмет: Алгебра,
автор: ОлЕг123312
Предмет: Математика,
автор: petrov456