Предмет: Алгебра,
автор: darkangelliveeangel
Найдите наименьшее значение функции а) y=3sinx - 10x + 3 и наибольшее значение ф-ции б) y=10cosx + 12x - 5 на промежутке [-3П (пи)/2; 0]
Ответы
Автор ответа:
0
................................................................
............................................................
............................................................
Приложения:
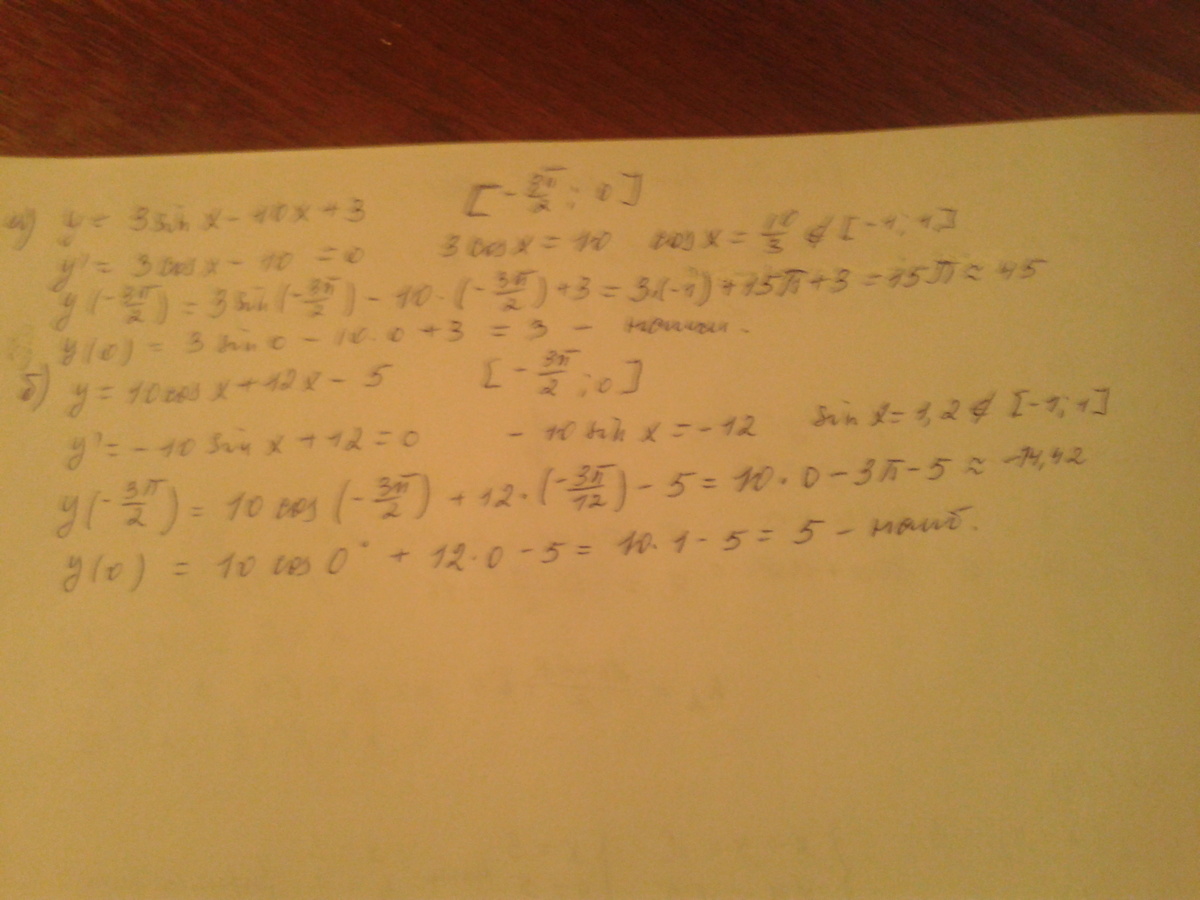
Автор ответа:
0
Ответ:
Объяснение:
Найдём стационарные точки. Для этого вычислим производную функции y и приравняем её к 0.
∉ [-1; 1] ⇒ стационарных точек нет
Подставим границы промежутка
Наименьшее значение функции на промежутке [-3π/2; 0] равно 3
∉ [-1; 1] ⇒ стационарных точек нет
Наибольшее значение функции на промежутке [-3π/2; 0] равно 5
Похожие вопросы
Предмет: Математика,
автор: zalgaszejnolla14
Предмет: История,
автор: bekbolotaltay
Предмет: Українська мова,
автор: fyyffffg
Предмет: География,
автор: IlyaNepeivoda
Предмет: Литература,
автор: piryakov1995