Предмет: Алгебра,
автор: sofaartamonova68
помогите решить логарифмическое уравнение
Приложения:
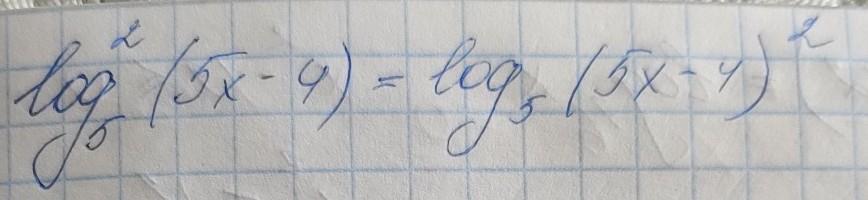
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Марина55555551
Предмет: Русский язык,
автор: tanywahrina
Предмет: Русский язык,
автор: дарья656
Предмет: Информатика,
автор: budykauульяна
Предмет: Қазақ тiлi,
автор: молдир57