Предмет: Математика,
автор: Viva8888
Решите уравнение/Solve an equation
Приложения:
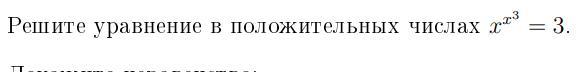
Ответы
Автор ответа:
0
Ответ:
(см. объяснение)
Пошаговое объяснение:
Угадываем корень . Покажем, что других корней исходное уравнение иметь не может. Сразу заметим, что
. Теперь прологарифмируем обе части равенства по основанию
:
. Так как
не является корнем уравнения, то
. Левая часть - возрастающая функция, правая - убывающая при
. Тогда
- единственный корень уравнения.
Уравнение решено!
Похожие вопросы
Предмет: Русский язык,
автор: schwirkowakat
Предмет: Русский язык,
автор: kate813
Предмет: Русский язык,
автор: Маша00711
Предмет: Физика,
автор: dyshevnoe
Предмет: Математика,
автор: yarikponomaryo