Предмет: Геометрия,
автор: ivanhenin009
В треугольнике ABC проведены высота AТ и биссектриса АМ . Найдите угол ТАМ , если угол ВАC равен 34° , угол ABC равен 46°.
Ответы
Автор ответа:
0
Ответ:
∠ТАМ = 27°
Объяснение:
Дано:
∠ВАС = 34°
∠АВС = 46°
АМ - биссектриса
АТ - высота
Найти:
∠ТАМ - угол между высотой и биссектрисой
Решение:
Найдём третий угол Δ АВС
∠АСВ = 180° - (∠ВАС + ∠АВС) = 180° - (34° + 46°) = 100°
Поскольку ∠АСВ тупой, то высота АТ опущена на продолжение стороны ВС, и
∠ТАМ = ∠ТАС + ∠САМ
∠ТСА = внешний угол про вершине С треугольника АВС, поэтому
∠ТСА = ∠ВАС + ∠АВС = 34° + 46° = 80°
Тогда поскольку АТ - высота, и ∠АТС = 90°, то
∠ТАС = 90° - ∠ТСА = 90° - 80° = 10°
∠САМ является половиной угла ВАС, так как АМ - биссектриса
∠САМ = 0,5 ∠ВАС = 0,5 · 34° = 17°
∠ТАМ = ∠ТАС + ∠САМ = 10° + 17° = 27°
Автор ответа:
0
Объяснение:
Решение на фото
____________________
Приложения:
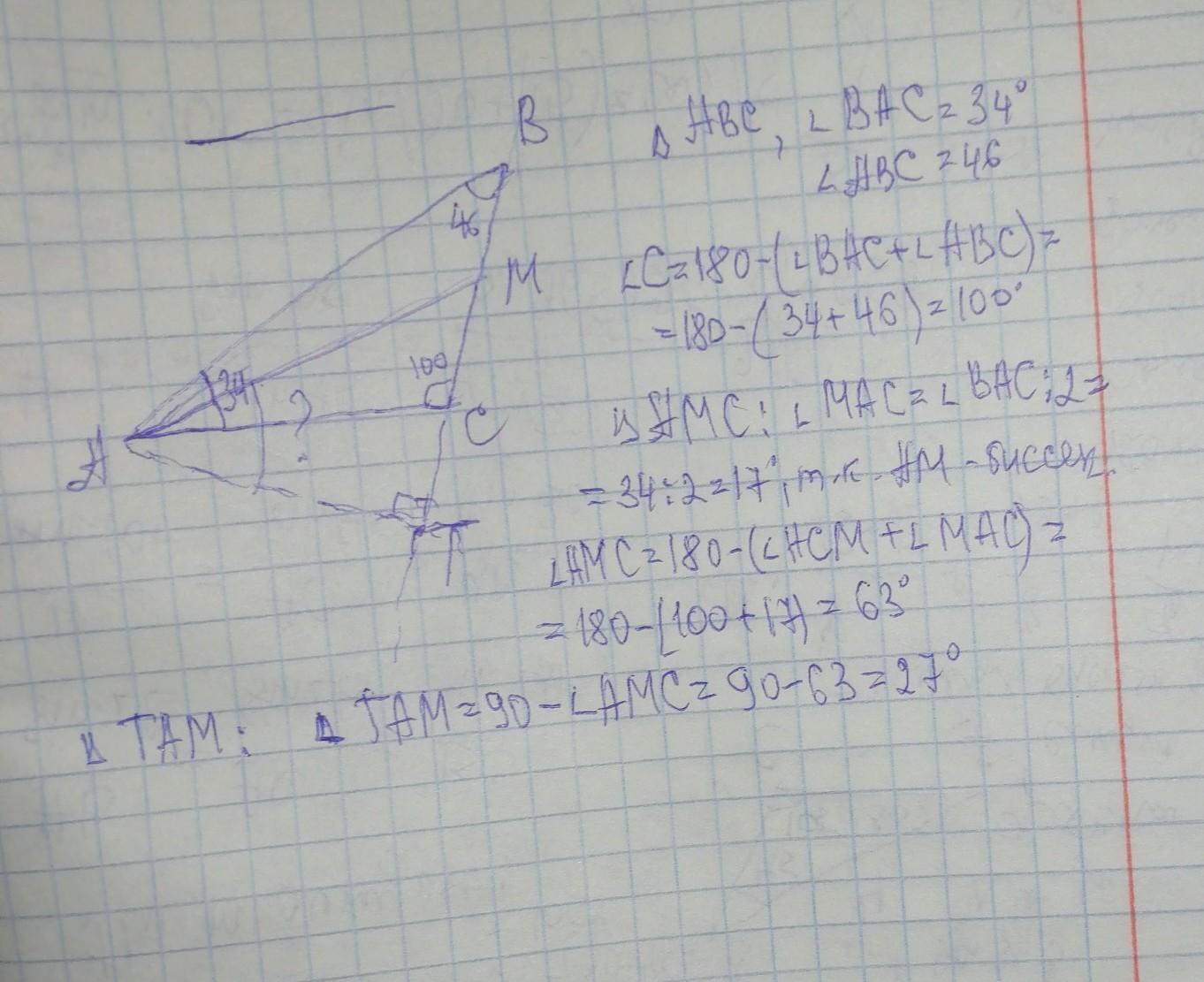
Похожие вопросы
Предмет: Английский язык,
автор: гарикбог
Предмет: Английский язык,
автор: Вероникаbonny
Предмет: Русский язык,
автор: НиНэЛь123
Предмет: Русский язык,
автор: mandarinkaaa15
Предмет: Алгебра,
автор: kshmil