Предмет: Математика,
автор: kr23m
Помогите доказать тождество
Приложения:
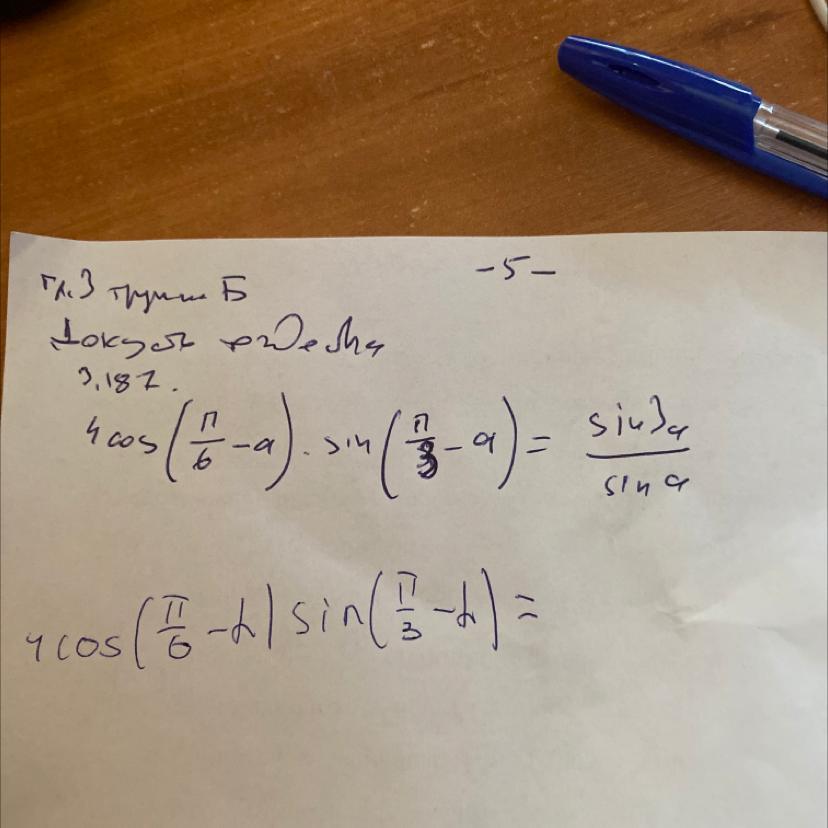
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
sinxcosy=0,5(sin(x-y)+sin(x+y))
sin(x+y)=sinxcosy+sinycosx
sin3a=sin(a+2a)=sinacos2a+sin2acosa=sinacos2a+2sinacosacosa=sina(cos2a+2cos²a)=sina(cos2a+1+2cos²a-1)=sina(cos2a+1+cos2a)=sina(1+2cos2a)
sin3a/sina=sina(1+2cos2a)/sina=1+2cos2a
ч.т.д
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: tata119
Предмет: Английский язык,
автор: kpp2017
Предмет: Окружающий мир,
автор: знанияточкаком2
Предмет: Математика,
автор: мишаоньо
Предмет: Русский язык,
автор: BlindKD