Question

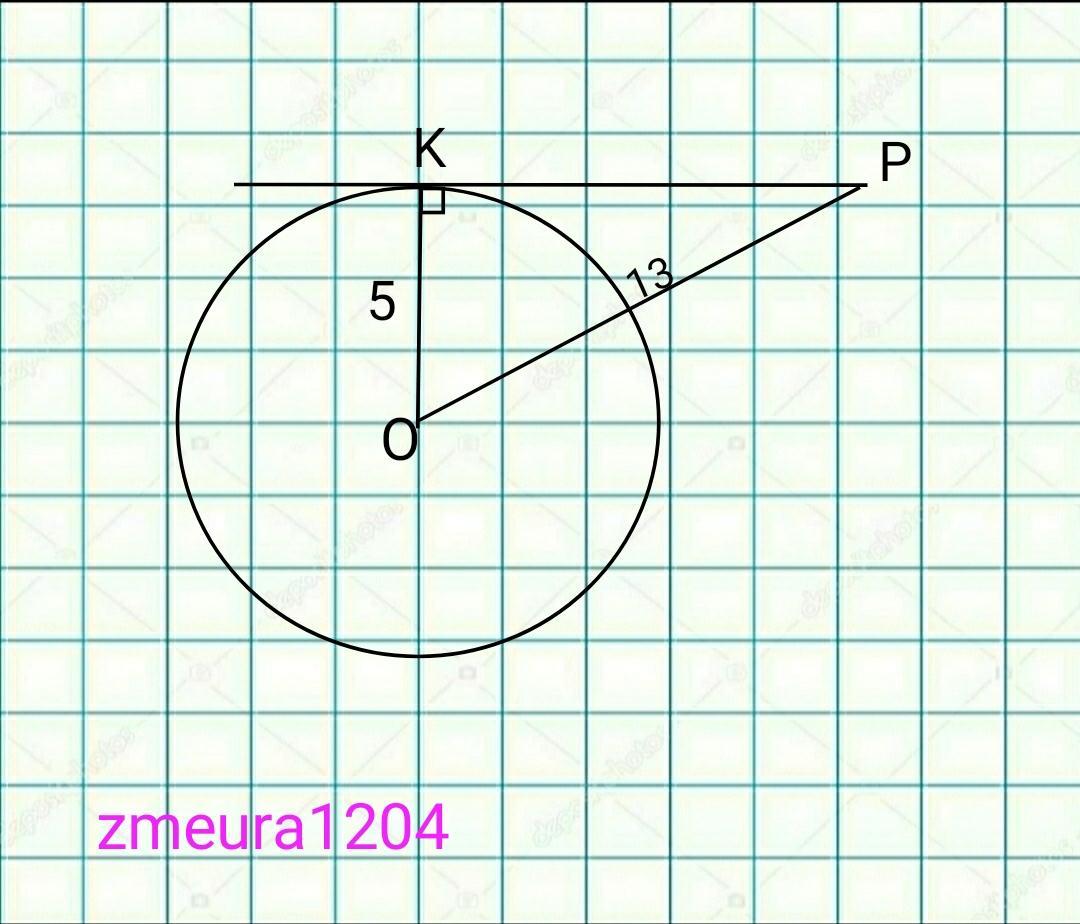
Срочно! Расстояние от точки P до центра O окружности ω радиуса 5 равно 13. Чему равна длина касательной, проведённой из P к ω?

Answer 1

Відповідь:

12

Пояснення:

за теоремою Піфагора шукана довжина дорівнює $\sqrt{13^2-5^2} = \sqrt{8*18} = 12$

Answer 2

Ответ:

12

Объяснение:

Дано:

РО=13 расстояние от точки Р до центра окружности.

ОК=R=5 радиус окружности

КР=? касательная к окружности.

Решение:

∆ОКР- прямоугольный треугольник

РО- гипотенуза

РК;КО - катеты.

По теореме Пифагора

РК=√(РО²-ОК²)=√(13²-5²)=√(169-25)=

=√144=12