Предмет: Математика,
автор: alexalexcov
Вычислить пределы функций:
Приложения:
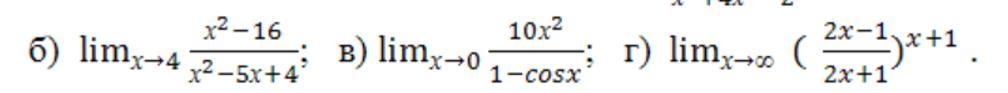
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: Unicorn14255
Предмет: Французский язык,
автор: misha2004sh
Предмет: Английский язык,
автор: 5000ss
Предмет: География,
автор: папа2234
Предмет: Окружающий мир,
автор: Maksimus465