Предмет: Геометрия,
автор: vlad8748
Даны точки A, B, C, лежащие на одной прямой, и точка P вне этой прямой. К отрезкам PA, PB, PC через их середины X, Y, Z проведём серединные перпендикуляры. Пусть они пересеклись в центрах Oa, Ob, Oc описанных окружностей треугольников PBC, PAC, PAB. Выберите на картинке 4 точки: 3 вершины треугольника и точку, лежащую на описанной окружности этого треугольника такие, что на картинке есть 3 точки, лежащие на прямой Симсона выбранной точки относительно выбранного треугольника. Все 7 точек должны быть различны.
Приложения:
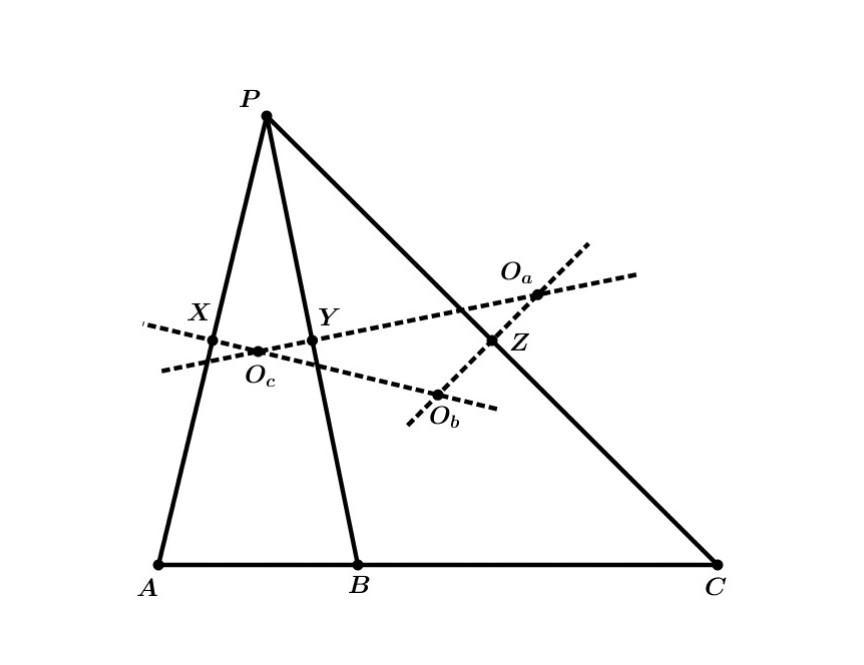
Ответы
Автор ответа:
1
ObX, ObZ - серединные перпендикуляры
ObXP =ObZP =90 => XPZOb - описанный четырехугольник (POb - диаметр)
То есть Ob лежит на описанной окружности треугольника XPZ.
X, Z - основания перпендикуляров из Ob к сторонам треугольника XPZ.
Тогда XZ - прямая Симсона точки Ob относительно треугольника XPZ.
XY - средняя линия в APB, XY||AC
YZ - средняя линия в BPC, YZ||AC
Через точку Y можно провести только одну прямую, параллельную AC => точки X-Y-Z лежат на одной прямой.
Приложения:
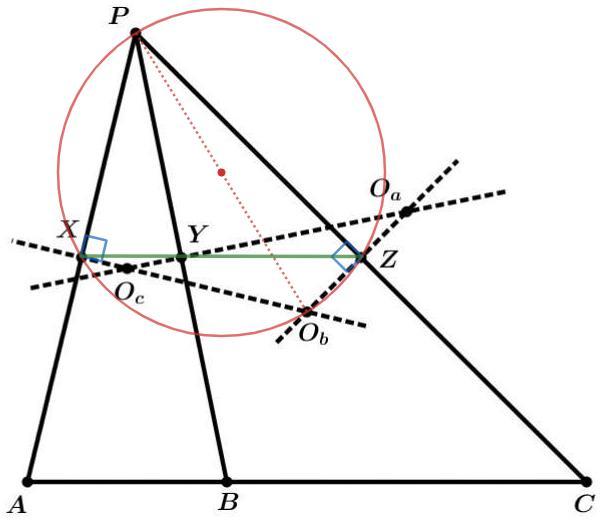
mishkarudo:
так какой ответ
это неверное решение
все 7 точек должны быть различны
i.imgur.com/FHmDxPy.png
Похожие вопросы
Предмет: Английский язык,
автор: kovalenyli
Предмет: Русский язык,
автор: Арешок
Предмет: Русский язык,
автор: соня20056
Предмет: Информатика,
автор: lonardit1
Предмет: Математика,
автор: Аксинья1111111111