Question

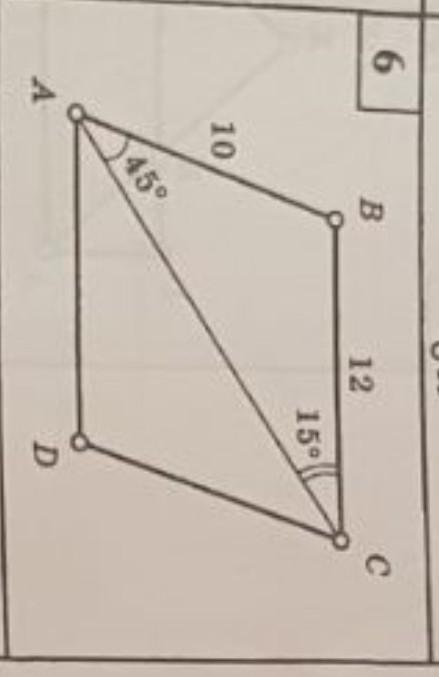
Надо найти площадь паралеллограмма​, 6 номер, даю 20 баллов

Answer 1

Відповідь:

$S = 60\sqrt{3}$

Пояснення:

проведём высоту BH, допустим к стороне AD, BC || AD и соответственно ∠BCA = ∠DAC = 15° => ∠DAB = 60° тогда sin∠BAH - sin60 = $\frac{BH}{AB} = \frac{\sqrt{3} }{2} => BH = \frac{\sqrt{3}*10 }{2} = 5\sqrt{3}$

площадь параллелограмма равна высоте на сторону, к которой она проведена, значит $S = 5\sqrt{3} * 12 = 60\sqrt{3}$ (AD = BC за св. пар.)

Answer 2

Ответ:

60√3 ед²

Объяснение:

∡В=180-45-15=120°

Проведем высоту ВН, Рассмотрим ΔАВН - прямоугольный.

∠АВН=120-90=30°

значит, АН=1/2 АВ=10:2=5

Найдем ВН по теореме Пифагора

ВН=√(АВ²-АН²)=√(100-25)=√75=5√3

S=AD*BH=12*5√3=60√3 ед²