Предмет: Алгебра,
автор: natalyapevchenko82
найдите наибольшее и наименьшее значения функции f(х)=х^3-3х^(2)-12х на отрезке -3;4
Ответы
Автор ответа:
0
Ответ:
Объяснение:
воспользуемся производной первого порядка
f'(x) = 3x²-6x-12
теперь критические точки
3x²-6x-12 = 0 ⇒ x₁ = 1+√5≈ 3.2 x₂=1-√5≈ -1.2 обе точки попадают в нужный отрезок
считаем значение функции в критических точках и на концах отрезка
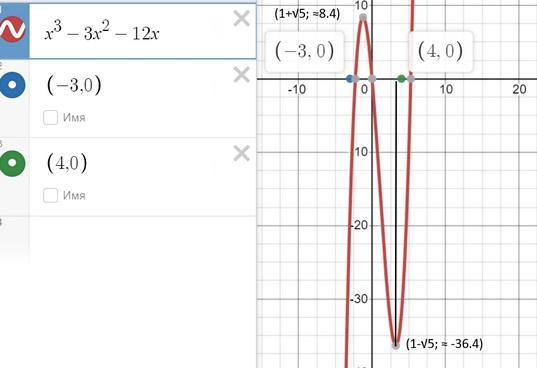
f(1+√5) ≈ -36.4
f(1-√5) ≈ 8.4
f(-3) = -18
f(4) = -32
ответ
fmin = f(1+√5) ≈ -36.4, fmax =f(1-√5) ≈ 8.4
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: sunrise20367
Предмет: Русский язык,
автор: Марусся1987
Предмет: Українська мова,
автор: souzviktan
Предмет: Математика,
автор: TopTan8120
Предмет: Обществознание,
автор: nadya8795