Question

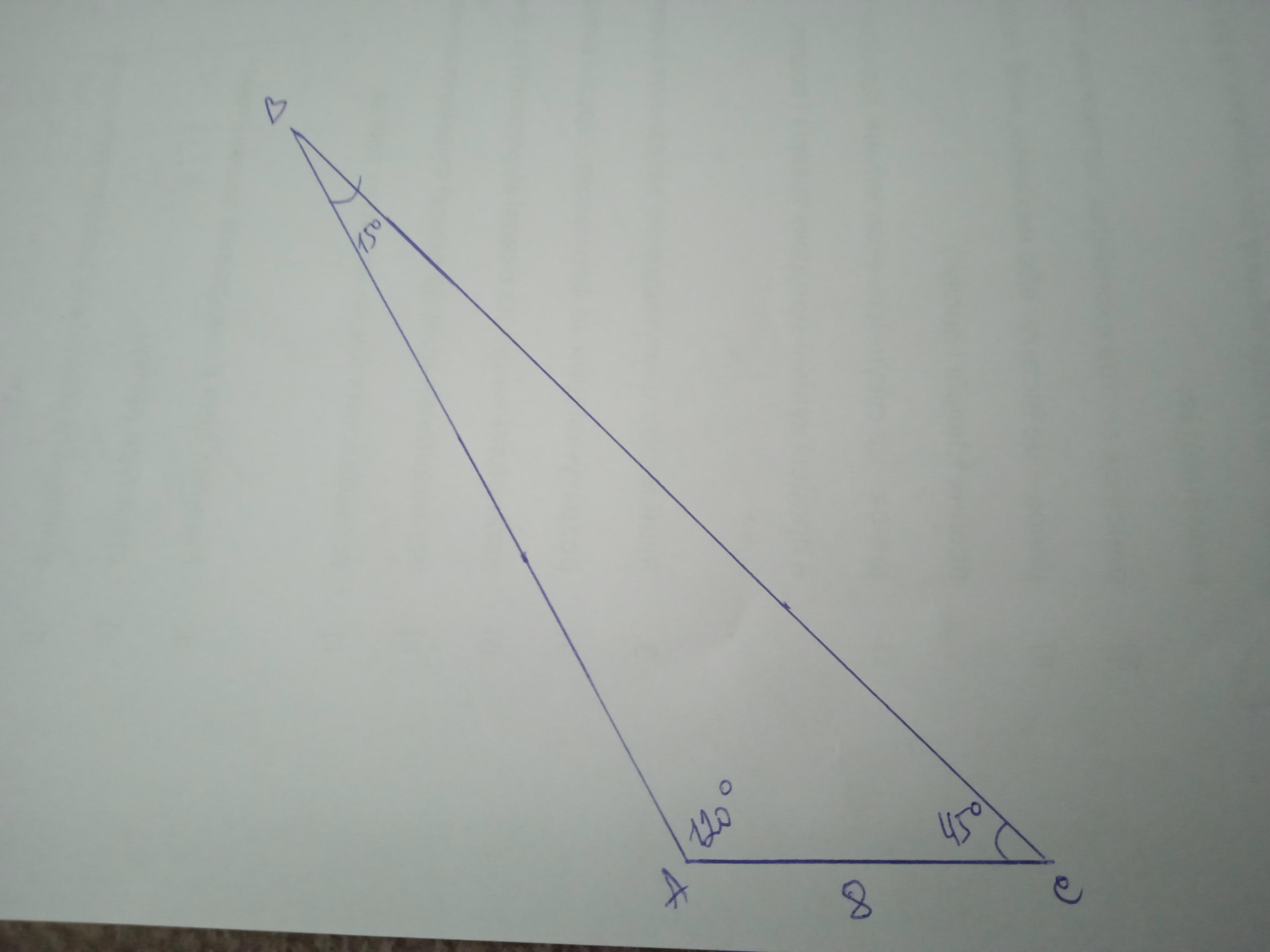
Два угла треугольника равны 45° и 120°, а сторона, лежащая против меньшего из них, равна 8. Найдите сторону треугольника, лежащую против большего из данных углов. Выполните рисунок к задаче и запишите подробное решение.

Answer 1

Два угла треугольника равны 45° и 120°, а сторона, лежащая против меньшего из них, равна 8. Найдите сторону треугольника, лежащую против большего из данных углов.

Объяснение:

Найдем третий угол , по т. о сумме углов треугольника

180°-120°-45°=15°.

Тогда углы в этом треугольники 120°, 45°, 15°.

Против угла 15°  лежит сторона 8 ед ,

против угла 120° пусть лежит сторона х ед.

Тогда по т. синусов  $\frac{8}{sin15} =\frac{x}{sin120}$ ,

Посчитаем синусы :sin15= sin(60-45)= sin60*cos45-sin45*cos60=$\frac{\sqrt{6} -\sqrt{2} }{4}$ ,

sin120= sin(90+30)=$\frac{\sqrt{3} }{2}$.

Тогда х= $8*\frac{\sqrt{3} }{2} :\frac{\sqrt{6} -\sqrt{2} }{4}=8*\frac{\sqrt{3} }{2}*\frac{4}{\sqrt{6}-\sqrt{2} }= \frac{16\sqrt{3} }{\sqrt{6}-\sqrt{2} }$ = 4√6(√3+1) .

Answer 2

Ответ:

4(√18+√6) cм

Объяснение:

Дано: ΔАВС, ∠А=120°, ∠С=45°,  АС=8 см. Найти ВС.

∠В=180-(120+45)=15°

По теореме синусов sinВ/AС=sinA/BC

BC=AС*sin120:sin15

sin15°=sin(60-45)=sin60*cos45-sin45*cos60=

=√3/2 * √2/2 - √2/2 * 1/2 = (√6-√2)/4

BC=8 * √3/2 : (√6-√2)/4  = (16√3 (√6+√2))/(√6-√2)(√6+√2)=

=16(√18+√6)/4=4(√18+√6) cм