Предмет: Алгебра,
автор: Noe1
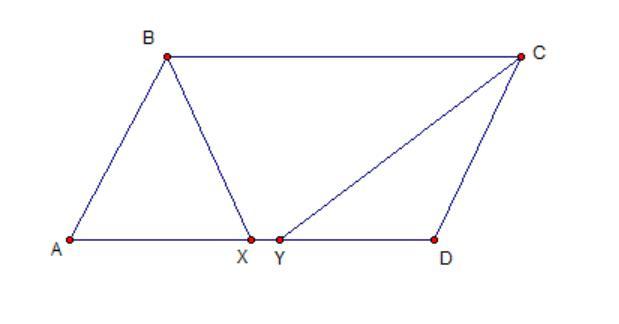
В параллелограмме ABCD сторона AB равна 6. Из вершин B и C проведены биссектрисы
углов, пересекающие сторону AD в точках X и Y соответственно. Найдите длину AD, если XY = 2.
Разберите все случаи.
Ответы
Автор ответа:
2
AB = CD = 6.
Поскольку BX и CY - биссектрисы, то ∠ABX = ∠XBC и ∠DCY = ∠YCB.
∠XBC = ∠BXA и ∠CYD = ∠YCB как накрест лежащие, следовательно, ΔABX и ΔCYD - равнобедренные ⇒ AB = AX = CD = DY = 6
AD = AX + XY + YD = 6 + 2 + 6 = 14
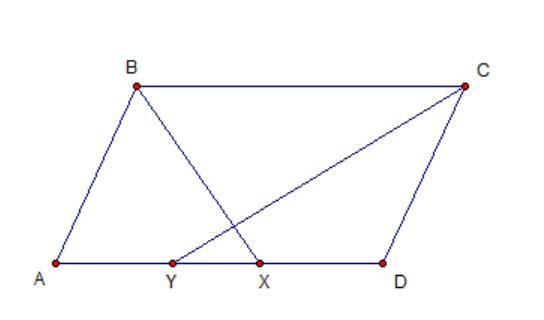
Рассмотрим второй случай, если BX и BY - пересекаются.
Поскольку BX и CY - биссектрисы, то ∠ABX = ∠XBC и ∠DCY = ∠YCB.
∠XBC = ∠BXA и ∠CYD = ∠YCB как накрест лежащие, следовательно, ΔABX и ΔCYD - равнобедренные ⇒ AB = AX = CD = DY = 6
AY = AX - YX = DY - YX = DX = 4
AD = AY + YX + XD = 4 + 2 + 4 = 10
Ответ: 14 или 10.
Приложения:
antonovm:
https://image.prntscr.com/image/IoQ8BIjmTq6g14VyNnOnyw.jpeg
Похожие вопросы
Предмет: Русский язык,
автор: wn2
Предмет: Русский язык,
автор: 2aalinaa2
Предмет: Русский язык,
автор: pyfybt1
Предмет: Обществознание,
автор: soldatovavika45
Предмет: Химия,
автор: trilaula