Предмет: Математика,
автор: 15sergei1966
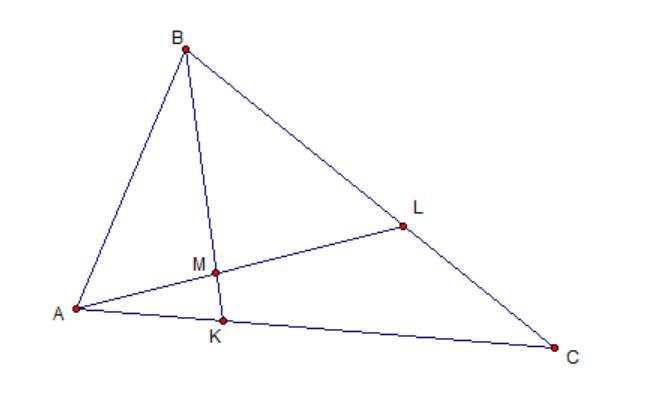
В треугольнике ABC на стороне AC отмечена точка К так,что AK:KC=3:5, на стороне BC -точке L так что, BL:LC=2:1.Отрезки AL и BK пересекаются в точке М.Найдите площадь треугольника ABM, если площадь треугольника ABC равна 38
Аноним:
В условии лишние данные присутствуют. Получилось S(ABM) = 76/3
Ошибся
Получается S(ABM) = 114/7 приблизительно 16, 3
Ответы
Автор ответа:
0
По теореме Менелая для треугольника BKC:
Рассмотрим отношение площадей треугольников ABC и ABL
Отношение площадей треугольников ABC и BKC:
Аналогично, рассмотрим отношение площадей треугольников BKC и MBL
отсюда найдём площадь треугольника ABM
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ник756
Предмет: Русский язык,
автор: Аноним
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: 1232905
Предмет: География,
автор: Sheludco8