Помогите пожалуйста сейчас надо
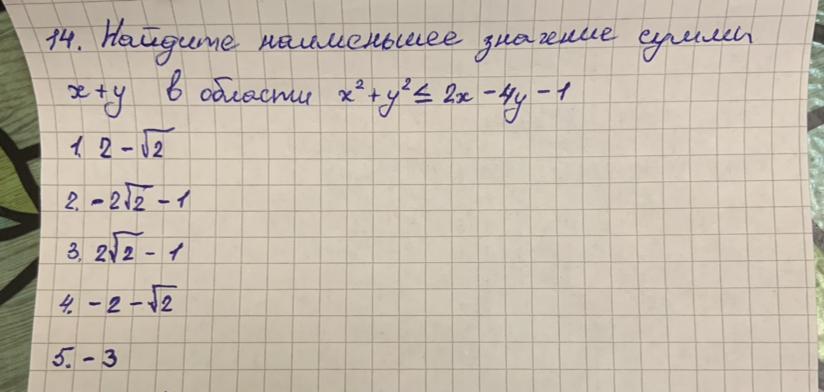
Ответы
Ответ:
2. -2√2 - 1
Пошаговое объяснение:
Пусть x + y = a. Тогда нужно найти наименьшее значение параметра a, при котором система
имеет хотя бы одно решение (то есть существует некоторая точка, при которой значение параметра, т. е. сумма, минимально возможное).
Рассмотрим неравенство:
Оно задаёт круг с центром (1; -2) и радиусом 2.
Рассмотрим равенство:
Оно задаёт прямую с коэффициентом k = -1. Изменяя параметр, мы передвигаем эту прямую вверх-вниз: чем меньше значение параметра, тем прямая ниже. Она может не пересекать круг, либо его касаться, либо пересекать. Нас интересует наименьшее значение параметра, то есть это касание круга снизу. Если возьмём меньше — общих точек не будет.
Найдём a, при которых достигается касание, с помощью уравнения соответствующей окружности:
Уравнение должно иметь один корень, так как точка касания одна, значит, его дискриминант (в том числе и дискриминант, делённый на 4, которым мы воспользуемся), равен нулю:
Наименьшее значение параметра —
