Предмет: Геометрия,
автор: vladimirsemeryuk
пусть в треугольнике abc стороны ab=5,bc=6,ca = 7. проведена касательная к окружности, вписанной в треугольник, параллельная стороне ac. Эта касательная отсекает треугольник BMN от данного треугольника ABC. Найти отношение радиусов вписанных окружностей в треугольники BMN и ABC
antonovm:
1 : 9 , задача решается устно , если использовать связь между полупериметром и касательными
нет , 2 : 9
Это НЕВЕРНО! Отношение равно 0,049384564, то есть около 1/20.
Виноват, это отношение треугольников.
Отношение площадей вписанных окружностей такое же: 0,413736474 8,37758041 = 0,049386154
Отношение радиусов верно: 2/9. 0,3629 / 1,632993162 = 0,22222.
Ответы
Автор ответа:
1
Ответ:
2 : 9
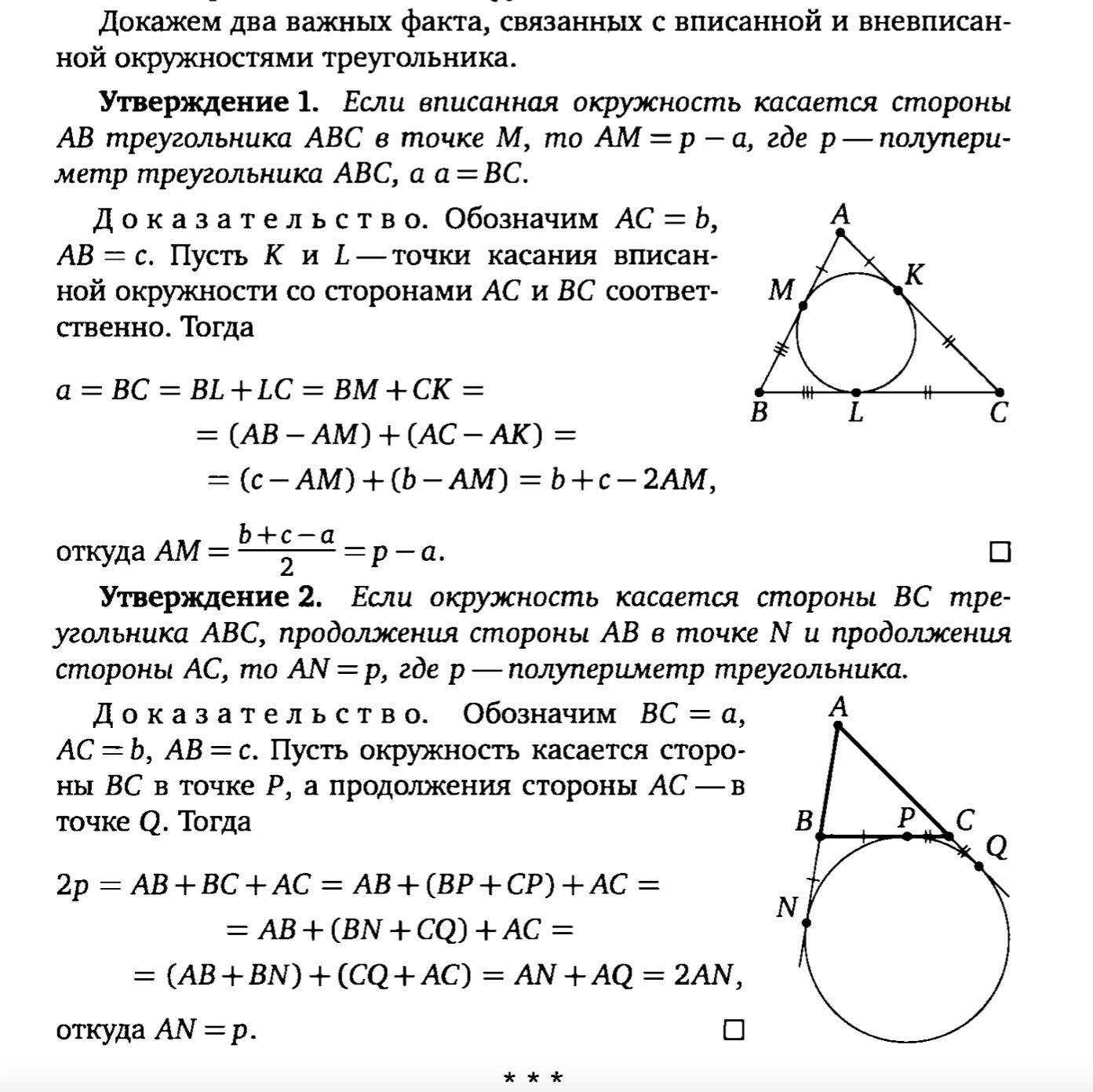
Объяснение: Добавил доказательство используемых утверждений ( Гордин ) , вообще для сдающих ЕГЭ его надо знать наизусть
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: ignatenko5
Предмет: Русский язык,
автор: polya641
Предмет: Русский язык,
автор: нате3
Предмет: Геометрия,
автор: akberovanar201
Предмет: Литература,
автор: gauhara1985