Предмет: Математика,
автор: vladimirsemeryuk
Решить данное уравнение:
Приложения:
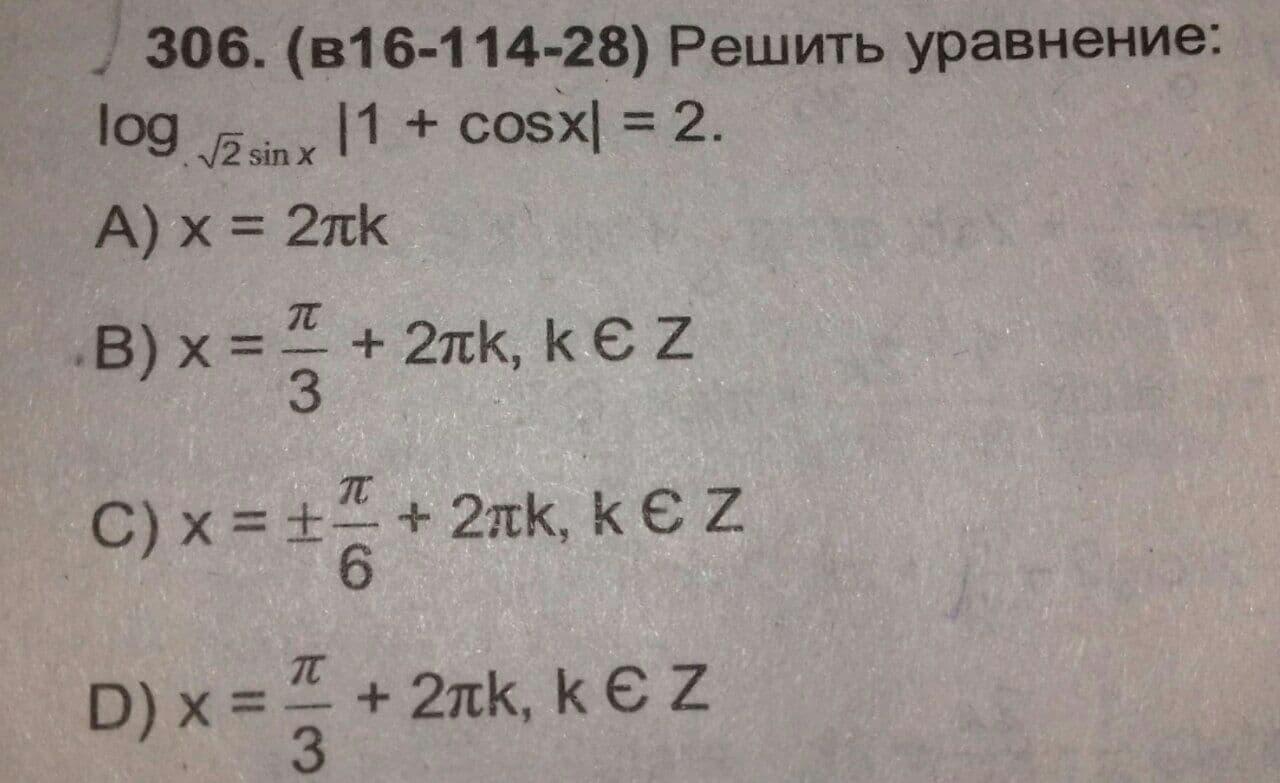
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
C учетом условий:
vladimirsemeryuk:
Спасибо! А почему из 2pi*k/3 мы перешли к 2pi*k в окончательном ответе?
Оставили только те точки, где синус положительный
Похожие вопросы
Предмет: Русский язык,
автор: cfcfcfcfcffffcfcfcfc
Предмет: Русский язык,
автор: Помощник111111111119
Предмет: Английский язык,
автор: kovalevakatyush2
Предмет: Русский язык,
автор: LeXonG