Предмет: Геометрия,
автор: liliannakramberi
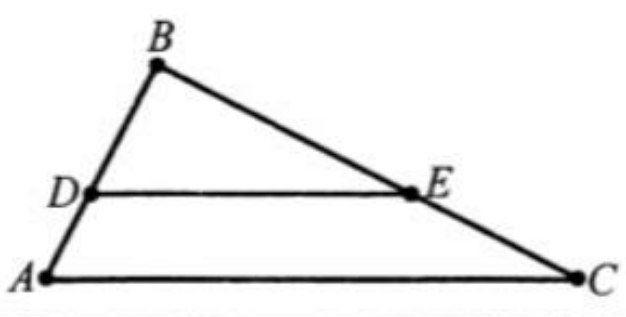
В треугольнике ABC отрезок DE с концами на сторонах AB и BC параллелен к стороне AC.  = 4 см²,
= 4 см²,  = 5 см²,
= 5 см²,  = 7 см. Найти длину AC.
= 7 см. Найти длину AC.
А) 9,5 см
Б)  см
см
В) 12 см
Г) 10,5 см
Д) 9 см
Приложения:
liliannakramberi:
Можно пожалуйста объяснение еще пожалуйста!!!!
По трем углам. Угол А равен углу D.
Это избыточные данные, их можно не учитывать для признака подобия
Ответы
Автор ответа:
2
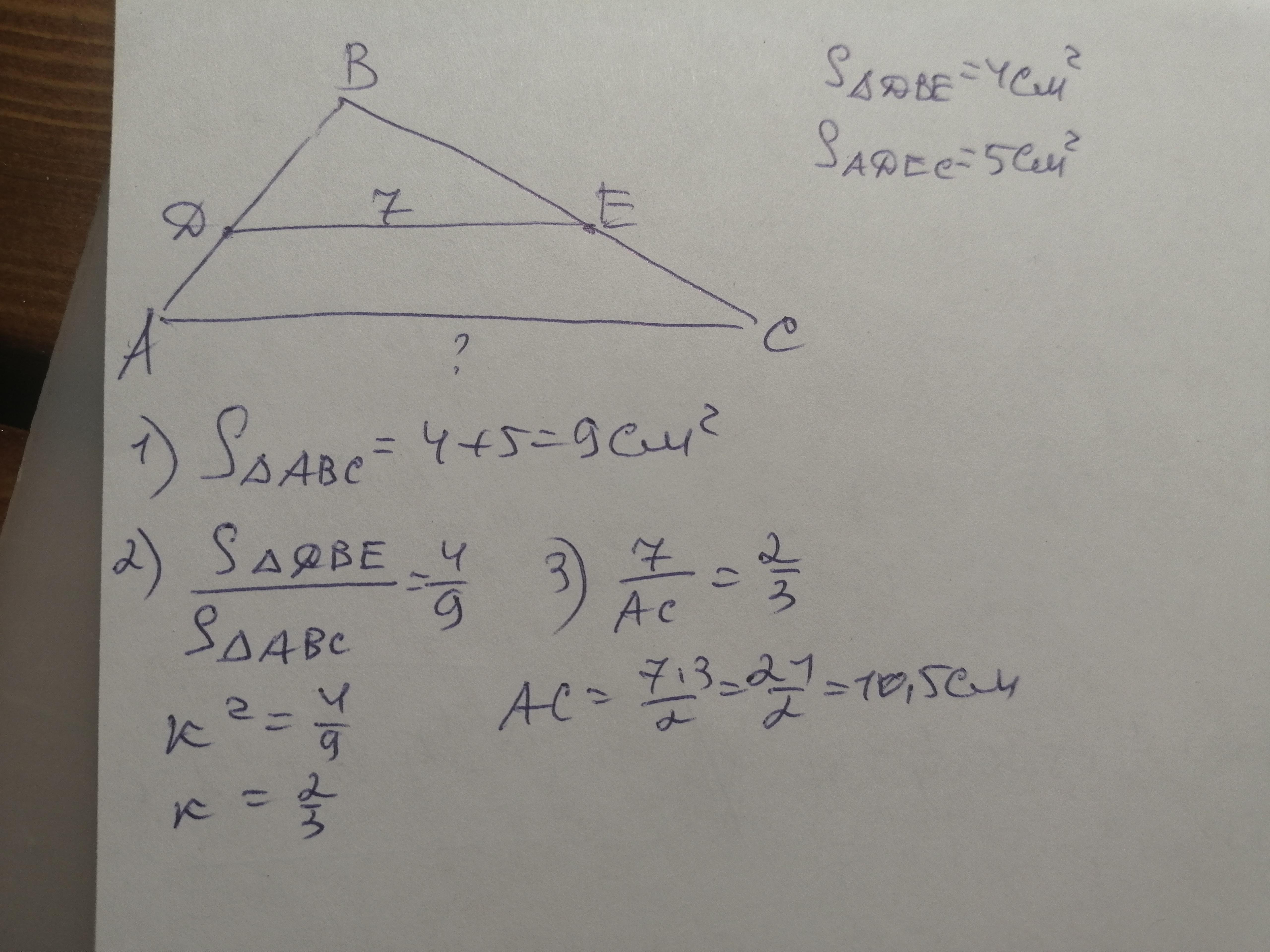
Ответ: Г
Объяснение:
Спасибо вам большое!!!! А откуда взялось 9?
4 + 5 = 9 см^2 - площадь треугольника АВС.
Теперь понял спасибо!!!!
Абсолютно верно
Автор ответа:
3
Ответ:
Объяснение:
Это ответ Г).
Приложения:
Помогите с геометрией пожалуйста вопрос в профиле
Похожие вопросы
Предмет: Английский язык,
автор: kovalevakatyush2
Предмет: Русский язык,
автор: Bella2222222
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: Egor38464847
Предмет: Русский язык,
автор: krist00807