Question

Объясните, как найти точку x₀ и производную в точке x₀

Answer 1

Ответ:

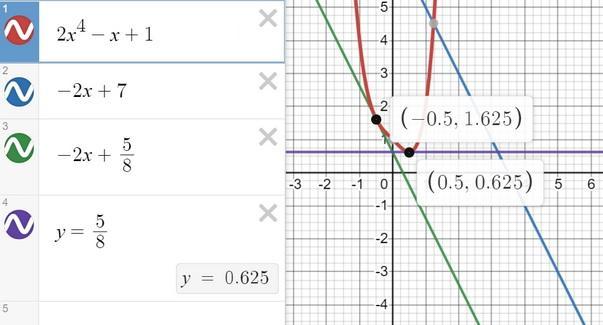
1) f'(x₀)=-2

2)x₀=-1/2

Пошаговое объяснение:

f'(x₀)=-2 (коэффициент при x в уравнении прямой)

f'(x)=2*4x³-1=8x³-1

8x³-1=-2

8x³=-1

x₀=-1/2

Answer 2

Ответ:

f'(x₀) = -2

x₀ = -0.5

Пошаговое объяснение:

у= kx+b

у нас есть уравнение прямой, которой должна быть параллельна касательная. значит у нас есть коэффициент  к при х для касательной

у = -2 *х +7

а этот коэффициент еще и значение производной функции в точке х₀

f'(x₀) = -2

значит, найдем производную и приравняем ее к -2, т.е  f'(x₀)= -2

(2x⁴ -x+1)' = 8x³ -1

8x₀³ -1 = -2   8x₀³ = -1  

$\displaystyle x_0=\sqrt[3]{-\frac{1}{8} } =\pm \frac{1}{2} =\pm 0.5$

таким образом мы получили две возможных точки,

проверим их

точка x₀= 0,5 f'(0.5) = 8*(0.5)³-1 = 0 в этой точке касательная не параллельна заданной прямой (более того, она параллельна оси ох, тк. коэффициент при х к=0)

точка x₀= 0,5 f'(0.5) = 8*(-0.5)³-1 = -2 в этой точке касательная параллельна заданной прямой

ответ

f'(x₀) = -2

x₀ = -0.5